一键解锁！梯形面积计算法，轻松get√

在探索数学世界的广阔天地里，梯形这一几何形状以其独特的形态和丰富的应用，成为了我们学习与生活中不可或缺的一部分。了解如何计算梯形的面积，不仅能够深化我们对几何学的理解，还能在实际问题中发挥重要作用，比如在设计、建筑、园艺乃至日常的手工制作中，都能找到它的身影。下面，我们就来详细探讨梯形面积的计算方法，确保每一步都清晰明了，让关键词“梯形面积”、“上底”、“下底”、“高”以及“计算方法”贯穿全文，帮助您更好地掌握这一知识点。

梯形面积的基本认识

首先，让我们明确梯形的定义：梯形是一组对边平行但另一组对边不平行的四边形。在这两组对边中，较长的平行边被称为梯形的“下底”，而较短的则被称为“上底”。而梯形中，从上底任一端点出发，垂直于下底（或延长线）的线段，我们称之为梯形的“高”。这三个要素——上底、下底和高，是计算梯形面积不可或缺的关键。

梯形面积的计算公式

当我们掌握了梯形的基本结构后，接下来便是学习如何运用这些要素来计算梯形的面积。幸运的是，数学家们已经为我们找到了一个简洁而高效的公式来完成这一任务。梯形面积的计算公式是：

\[ \text{面积} = \frac{1}{2} \times (\text{上底} + \text{下底}) \times \text{高} \]

这个公式背后的逻辑相当直观：首先，我们取上底和下底的平均长度，然后乘以梯形的高，最后得到的结果再除以2，即为我们所求的梯形面积。通过这种方式，无论梯形的大小、形状如何变化，我们都能准确地计算出它的面积。

计算步骤详解

为了更好地应用这个公式，我们可以将其分解为以下几个步骤：

1. 确定上底和下底：首先，明确梯形的上底和下底长度。在图中，这两条边是平行的，并且下底通常比上底长。

2. 找到梯形的高：从梯形的上底任一端点作垂直于下底（或其延长线）的线段，这条线段的长度就是梯形的高。注意，高应该是从上底到下底（或其延长线）的垂直距离。

3. 应用公式计算：将已知的上底、下底和高代入梯形面积的计算公式中。即先计算上底与下底之和，然后乘以高，最后将得到的结果除以2。

实例演练

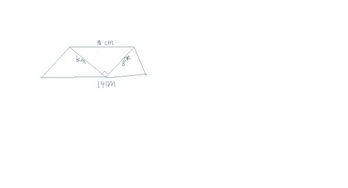
假设我们有一个梯形，其上底长度为4单位，下底长度为6单位，高为3单位。我们可以按照以下步骤来计算它的面积：

首先，计算上底与下底之和：\(4 + 6 = 10\)单位。

然后，将这个和乘以梯形的高：\(10 \times 3 = 30\)单位²（注意，这里我们还没有完成面积的计算，因为还需要除以2）。

最后，将上一步的结果除以2，得到梯形的面积：\(\frac{30}{2} = 15\)单位²。

所以，这个梯形的面积是15单位²。

梯形面积计算的应用

了解梯形面积的计算方法后，我们可以将其应用于各种实际情境中。比如，在设计一个梯形形状的花坛时，我们可以先测量出花坛的上底、下底和高，然后使用梯形面积的计算公式来确定所需的花草面积。同样地，在建筑领域，当需要估算梯形屋顶的覆盖材料面积时，这一公式也显得尤为重要。

结语

综上所述，通过掌握梯形面积的计算公式及其应用步骤，我们能够轻松应对与梯形面积相关的各种计算问题。无论是在理论学习还是实际应用中，这一知识点都扮演着重要的角色。希望本文的详细介绍能够帮助您更好地理解梯形面积的计算方法，并在实践中灵活运用，让数学的智慧为您的生活和工作增添更多便利与乐趣。