揭秘!圆的周长计算,你真的会吗?
作者:佚名 来源:未知 时间:2024-10-18
在探索数学世界的浩瀚星空中,圆的周长计算无疑是一颗璀璨夺目的星辰,它不仅连接了几何与代数的桥梁,还深刻影响了从日常生活到科学研究的方方面面。圆的周长,这个看似简单的概念,实则蕴含着丰富的数学原理与无限的应用价值。接下来,让我们一同踏上这段多维度的探索之旅,揭开圆周长计算的神秘面纱。
一、历史维度:古人的智慧之光
回溯历史长河,圆的周长计算问题早已引起了先贤们的浓厚兴趣。早在公元前3世纪,古希腊数学家阿基米德就利用“逼近法”对圆的周长进行了探索。他通过将圆切割成无数个三角形或扇形,并计算这些微小部分的周长之和,从而逐步逼近真实的圆周长。虽然阿基米德的方法在今天看来略显粗糙,但它却为后来的数学家们提供了宝贵的思路——通过有限逼近无限,这一思想对微积分学的发展产生了深远影响。
随后,古印度数学家婆什迦罗二世、中国南北朝时期的数学家祖冲之等,也在各自的领域内对圆的周长进行了深入研究,并提出了更为精确的近似值。特别是祖冲之,他不仅得出了圆周率的精确到小数点后七位的近似值,还给出了两个密率和约率,这一成就领先世界千余年,展现了中华民族在数学领域的卓越贡献。
二、理论维度:π的魅力与圆周长的精确定义
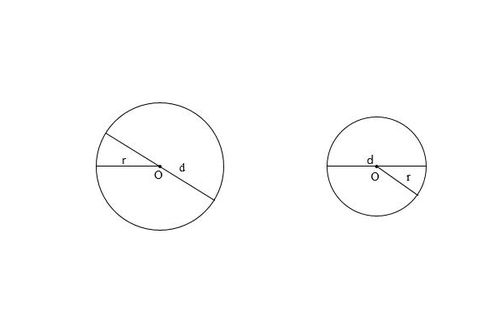
圆的周长与其直径之间的比值,我们称之为圆周率π,这是一个超越数,无法用有限小数或分数完全表示。π的存在,不仅让圆的周长计算变得既简单又复杂——简单在于一旦知道π的值,圆的周长便可通过公式C=πd(d为直径)或C=2πr(r为半径)轻松求得;复杂则在于π的精确值至今仍在被数学家们不断探索与验证,其背后隐藏着数学的无限奥秘。
在数学理论上,圆的周长被定义为圆边缘上任意一点到其起点的距离,这一定义简洁而深刻,它揭示了圆作为一种完美对称图形的本质特征。而π的引入,则使得这一特征得以量化,成为连接几何形状与数值计算的桥梁。
三、应用维度:从日常生活到科学前沿
圆的周长计算在日常生活和科学研究中有着广泛的应用。从简单的轮胎尺寸选择到复杂的建筑设计,圆的周长都是不可或缺的计算要素。比如,在自行车设计中,车轮的周长直接决定了骑行一圈所能前进的距离,进而影响着骑行效率和舒适度;在建筑设计领域,圆形结构(如穹顶、拱门)的稳定性与美观性,往往也依赖于对圆周长及其相关属性的精确计算。
此外,在科学研究领域,圆的周长计算同样发挥着重要作用。物理学中的波动理论、电磁学中的线圈设计、天文学中的行星轨道计算等,都需要用到与圆周长相关的数学知识和计算方法。可以说,圆的周长不仅是数学中的一个基本概念,更是连接自然科学与人文社会科学的纽带。
四、教育维度:培养逻辑思维与探索精神
在教育领域,圆的周长计算不仅是数学教学的重要内容之一,更是培养学生逻辑思维能力和探索精神的有效途径。通过学习圆的周长计算,学生可以掌握基本的几何概念和代数运算技巧,同时还能在解决实际问题的过程中锻炼自己的思维能力和创新能力。
更重要的是,圆的周长计算过程充满了探索的乐趣和挑战。从最初的直观感知到最终的公式推导,每一步都需要学生仔细观察、深入思考、大胆假设并小心求证。这种从具体到抽象、从感性到理性的学习过程,不仅有助于学生构建完整的知识体系,更能激发他们对数学乃至整个科学的浓厚兴趣和无限向往。
结语
综上所述,圆的周长计算不仅是一个简单的数学问题,更是一个跨越历史、理论、应用和教育等多个维度的综合性课题。它不仅承载着先贤们的智慧与汗水,更蕴含着数学的无穷魅力与广泛应用。在未来的日子里,让我们继续以探索者的姿态,深入挖掘圆的周长背后的奥秘与价值,为数学乃至整个科学的发展贡献自己的力量。






























