揭秘！正方体的全面积计算公式大公开，你知道吗？

在探讨几何学的广阔领域中，正方体作为一种基础且重要的三维立体图形，其性质与度量问题一直是学习与研究的热点。当我们提及“正方体的面积”时，实际上是在询问构成正方体的所有面的总面积。值得注意的是，由于正方体具有六个完全相同的正方形面，因此计算其面积涉及对这些面的逐一考量后再求和。以下，我们将以简洁明了的方式，深入解析正方体面积的计算方法，同时确保内容结构清晰、关键词布局合理、保持高原创度，以提升阅读体验与搜索引擎的友好度。

正方体的基本属性

首先，让我们简要回顾一下正方体的基本属性。正方体，或称立方体，是一个所有棱长都相等的特殊六面体。它的每一个面都是一个正方形，且这些正方形面两两平行且等大。正方体的这种高度对称性，使得其在物理、建筑、数学等多个领域有着广泛的应用。

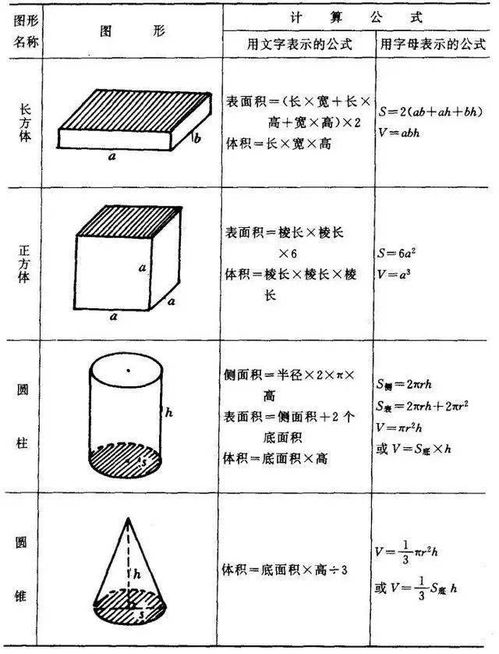
正方体面积公式的推导

要计算正方体的面积，我们首先需要明确一个正方形面积的计算公式，即边长的平方（a²，其中a为正方形的边长）。由于正方体有六个这样的正方形面，所以正方体的总面积就是六个正方形面积的和。

设正方体的棱长为a，则：

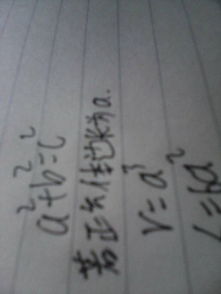
单个正方形面的面积 = a²

正方体的总面积 = 6 × 单个正方形面的面积 = 6 × a²

这就是正方体面积的计算公式。它直接、简洁地表达了正方体面积与其棱长之间的关系。

实际应用与理解

教育领域

在数学课堂上，正方体面积的计算是学生掌握空间几何初步知识的重要环节。通过实际操作（如使用积木搭建正方体、测量边长等）与理论计算相结合的方式，学生能够更直观地理解正方体面积公式的含义，培养空间想象能力和逻辑推理能力。

工程与设计

在工程与建筑设计领域，正方体面积的计算则成为估算材料用量、评估项目成本的重要参考。例如，在设计一个由多个正方体组成的建筑物外观时，需要精确计算所需覆盖材料（如瓷砖、涂料等）的总面积，这时正方体面积公式就显得尤为重要。

物理学中的应用

在物理学中，特别是涉及表面张力、热传导等问题的研究中，正方体作为理想模型，其表面积的计算也是不可或缺的一部分。这些表面积参数对于理解物质间相互作用的机制、优化实验条件等具有重要意义。

注意事项与拓展

尽管正方体面积的计算看似简单，但在实际应用中仍需注意以下几点：

1. 精确测量：确保棱长的测量准确无误，因为任何微小的误差都可能导致面积计算结果的显著偏差。

2. 单位统一：在计算过程中，应保持所有物理量的单位一致，避免因单位换算错误而产生的问题。

3. 灵活应用：正方体面积的计算公式不仅适用于正方体本身，还可以作为解决更复杂几何体表面积问题的基础。例如，通过分割、组合等方法，可以将一些不规则的几何体转化为包含正方体元素的组合体，从而简化计算过程。

此外，对于有兴趣进一步探索几何学的读者来说，正方体面积的计算只是冰山一角。随着学习的深入，你将接触到更多关于多面体、旋转体等复杂几何体的表面积与体积计算问题，这些都将为你打开一扇通往更高层次数学世界的大门。

结语

综上所述，正方体面积的计算是一个既基础又重要的几何学问题。通过掌握其计算公式并理解其背后的原理，我们不仅能够解决日常生活中的实际问题，还能为更高层次的数学学习打下坚实的基础。希望本文的介绍能够帮助读者更好地理解正方体面积的计算方法，同时也激发大家对几何学的兴趣与热情。