揭秘！log究竟是怎样一种神秘函数？

log是什么函数：揭开对数函数的神秘面纱

在数学的浩瀚宇宙中，函数如星辰般璀璨，而“log”函数，即对数函数，无疑是其中一颗引人注目的明星。它不仅是数学分析的重要工具，也是科学计算、工程技术和经济学等多个领域不可或缺的钥匙。今天，就让我们一起走进对数函数的世界，揭开它神秘而迷人的面纱。

一、初识对数函数：定义与起源

定义篇：首先，让我们从最基本的定义开始。对数函数（Logarithmic Function）是以幂（真数）为自变量，指数为因量，底数为常量的函数。简单来说，如果$a^x = N$（$a > 0$，且$a \neq 1$），那么数$x$叫做以$a$为底$N$的对数，记作$x = \log_a N$。这里，$a$是底数，$N$是真数，$x$是对数值。

起源篇：对数函数的诞生，可以追溯到17世纪的苏格兰数学家约翰·纳皮尔（John Napier）。为了简化大数的乘除法计算，纳皮尔发明了“对数”这一概念，并制作了第一张对数表《奇妙的对数表的描述》。随后，莱布尼茨、欧拉等数学巨匠进一步发展和完善了对数理论，使其成为现代数学中不可或缺的一部分。

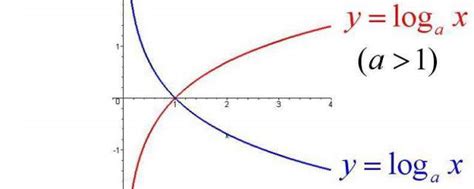
二、对数函数的性质：探索其奥秘

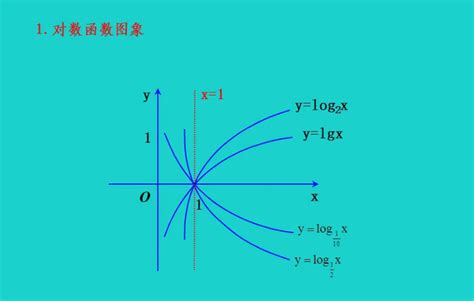
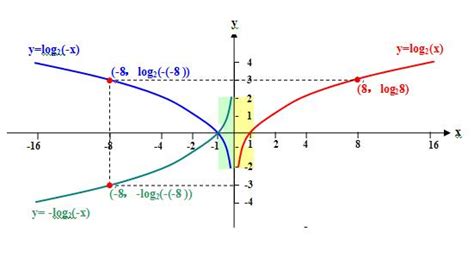
单调性：对数函数在其定义域内是单调的。对于底数大于1的对数函数（如$\log_2 x$），它是增函数；而对于底数在0到1之间的对数函数（如$\log_{\frac{1}{2}} x$），则是减函数。这一性质使得对数函数在解决不等式问题时特别有用。

换底公式：$\log_b N = \frac{\log_a N}{\log_a b}$，这一公式允许我们将任何底数的对数转化为以特定底数（如10或e）的对数，极大地扩展了对数函数的应用范围。

运算法则：对数函数还遵循一系列运算法则，如$\log_a (mn) = \log_a m + \log_a n$（积的对数等于对数的和），$\log_a \frac{m}{n} = \log_a m - \log_a n$（商的对数等于对数的差），以及$\log_a m^n = n\log_a m$（幂的对数等于对数的倍数）。这些法则简化了复杂表达式的处理。

三、对数函数的应用：从生活到科研

声音强度与分贝：在日常生活中，对数函数的一个直接应用是声音强度的测量。分贝（dB）是一种对数单位，用于量化声音相对于某个参考水平的强度。这种表示方式能够更有效地反映人耳对声音强度的感知差异。

经济学中的复利计算：在金融领域，对数函数与复利计算紧密相连。复利增长遵循指数规律，而对数函数则成为分析这种增长模式的有力工具。例如，通过求解对数方程，可以计算出达到特定金额所需的时间或利率。

科学研究与数据分析：在科学研究中，对数函数常用于处理那些具有指数增长或衰减特性的数据，如人口增长、放射性衰变等。此外，在统计学和数据分析中，对数变换能够帮助稳定数据的方差，使其更适合进行线性回归等分析。

计算机科学与算法复杂度：在计算机科学中，对数函数与算法复杂度的分析息息相关。算法的时间复杂度或空间复杂度常以对数形式表示，这反映了算法效率随输入规模增长而变化的趋势。例如，二分查找算法的时间复杂度为$O(\log n)$，表明其效率远高于线性查找。

四、结语：对数函数的魅力无限

综上所述，对数函数不仅是一种抽象的数学概念，更是连接现实世界与科学研究的桥梁。从日常生活中的声音强度测量，到经济学中的复利计算，再到科学研究与计算机科学的各个领域，对数函数都展现出了其独特的魅力和广泛的应用价值。正如数学家欧拉所言：“对数函数将一切事物都连接起来了。”让我们继续探索和学习对数函数，发现更多隐藏在其中的奥秘和乐趣吧！