揭秘长方体体积计算的奥秘：轻松几步，掌握空间度量精髓！

在探索三维世界的奇妙之旅中，有一个简单而强大的数学工具，它能帮助我们轻松揭开形状背后的秘密——那就是长方体的体积计算。想象一下，你正站在一个宽敞明亮的仓库前，里面堆满了各式各样的货物箱，它们都是完美的长方体形状。如何快速估算出这些箱子总共占据了多少空间？或者，如果你是一位建筑师，正计划设计一座充满创意的建筑，又该如何确保每个房间的大小既实用又符合美学？答案，就藏在长方体体积的计算之中。

揭开长方体体积的神秘面纱

首先，让我们从基础开始。长方体，这个我们日常生活中随处可见的几何体，以其简洁的线条和稳定的结构赢得了广泛的青睐。它由三组平行的矩形面组成，每组面都相互垂直。这不仅仅是一个简单的形状定义，更是我们理解其体积计算的关键所在。

体积，空间的量化艺术

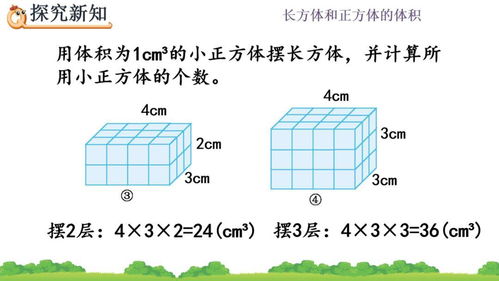
体积，简而言之，就是物体所占空间的大小。对于长方体而言，体积的计算就是将其长度、宽度和高度的三个维度相乘。这个过程，就像是在进行一场三维的乘法游戏，每一次的相乘都让我们更加接近那个隐藏在形状背后的数字——体积。

动手实践：计算长方体的体积

第一步：认识长方体的三个维度

拿起你的尺子或者想象一个长方体，仔细观察它的三个主要尺寸：

长度（L）：从长方体的一端到另一端的最大距离。

宽度（W）：与长度垂直，但同样是从一端到另一端的距离。

高度（H）：垂直于长度和宽度的方向上的距离，也就是长方体的“厚度”。

第二步：执行乘法运算

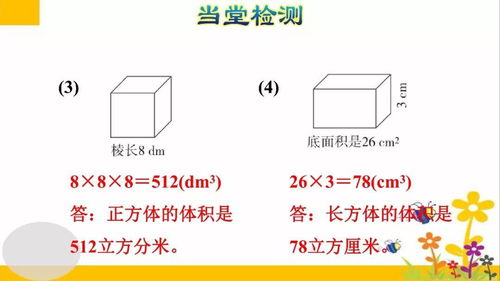
现在，是时候展现你的数学魔力了！将这三个尺寸相乘，得到的结果就是长方体的体积（V）。公式如下：

\[ V = L \times W \times H \]

举个例子，假设你有一个长为5米、宽为3米、高为2米的长方体房间。根据公式，其体积为：

\[ V = 5 \text{米} \times 3 \text{米} \times 2 \text{米} = 30 \text{立方米} \]

这意味着，这个房间内部的空间总量是30立方米，足够容纳许多家具和装饰品，为你打造一个温馨舒适的家。

深入探索：为什么这个公式有效？

或许你会好奇，为什么仅仅是三个尺寸的乘积就能代表长方体的体积呢？这背后其实蕴含着几何学的深刻原理。想象一下，如果你把长方体切成无数个小立方体（每个小立方体的边长都非常小），那么这些小立方体的总体积加起来，就约等于原长方体的体积。而每个小立方体的体积就是其边长的三次方（因为立方体也是长方体的一种特殊形式，三个维度相等）。因此，当我们把长方体看作是由许多这样的小立方体组成时，其总体积就可以通过计算这些小立方体的数量（即长度、宽度和高度的乘积）来得到。

应用场景：从日常生活到专业领域

长方体体积的计算，不仅仅是一个数学游戏，它在我们的日常生活中有着广泛的应用。从家居装修时的材料估算，到物流运输中的空间规划，再到建筑设计中的空间布局，都离不开对体积的精确计算。此外，在科学研究、工程设计、农业生产等多个领域，长方体体积的计算也是一项基本技能，它帮助人们更好地理解和利用三维空间。

结语

通过这次对长方体体积计算的探索，我们不仅学会了如何运用一个简单的公式来量化三维空间的大小，还深刻体会到了数学与现实生活之间的紧密联系。长方体的体积计算，就像是一把钥匙，为我们打开了一个充满无限可能的三维世界。无论是为了日常生活中的便利，还是为了专业领域的发展，掌握这项技能都将使我们受益匪浅。所以，下次当你再次遇到长方体时，不妨试着用你新学到的知识去估算它的体积吧！你会发现，数学，其实就在我们身边，等待着我们去发现、去应用、去享受它带来的乐趣。