如何计算长方体的体积？

在探索几何学的广阔天地中，长方体作为三维空间中最基础且常见的形状之一，其体积的计算是理解三维空间度量关系的重要一环。无论是日常生活中的包装盒、房间布局，还是建筑工程中的结构设计，长方体体积的计算都扮演着不可或缺的角色。本文将深入浅出地介绍长方体体积的计算方法，旨在帮助读者全面理解并掌握这一基础知识。

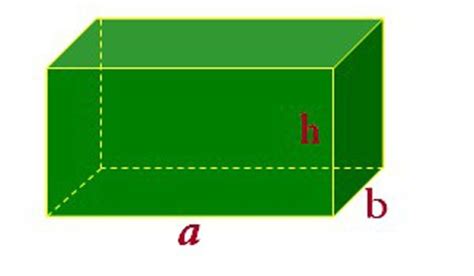
一、长方体的基本认识

首先，让我们从长方体的基本定义开始。长方体，顾名思义，是一个具有六个矩形面的三维几何体，其中相对的两个面是完全相同的。它有三个维度：长度（L）、宽度（W）和高度（H），这三个维度决定了长方体的大小和形状。

二、体积的概念

在深入探讨长方体体积的计算之前，理解“体积”这一概念至关重要。体积是描述三维空间内物体占据空间大小的一个量度，其单位是立方单位（如立方厘米、立方米等）。简单来说，体积就是物体内部所包含的空间大小。

三、长方体体积的计算公式

长方体体积的计算基于其三个维度：长度、宽度和高度。通过这三个参数的乘积，我们可以得到长方体的体积。具体公式如下：

\[ \text{体积} = \text{长度} \times \text{宽度} \times \text{高度} \]

或者，用数学符号表示为：

\[ V = L \times W \times H \]

其中，V代表体积，L代表长度，W代表宽度，H代表高度。

四、计算步骤示例

为了更好地理解如何应用上述公式，我们通过一个具体的例子来展示计算过程。

例题：一个长方体的长为5厘米，宽为4厘米，高为3厘米，求其体积。

解题步骤：

1. 识别参数：首先，明确长方体的三个维度参数，即长度L=5厘米，宽度W=4厘米，高度H=3厘米。

2. 应用公式：将上述参数代入体积公式中，即 \( V = L \times W \times H \)。

3. 执行计算：进行乘法运算，\( V = 5 \text{厘米} \times 4 \text{厘米} \times 3 \text{厘米} = 60 \text{立方厘米} \)。

4. 得出结论：因此，该长方体的体积为60立方厘米。

五、实际应用场景

长方体体积的计算在日常生活和工作中有着广泛的应用。以下列举几个常见的应用场景：

1. 包装与物流：在物流行业，计算货物的体积对于合理安排运输空间、预估运费等至关重要。通过测量货物的长、宽、高，即可快速计算出其体积，从而进行高效的物流管理。

2. 建筑设计：在建筑设计中，设计师需要精确计算各种材料（如砖块、混凝土等）的体积，以确保施工过程中的材料使用既不过剩也不短缺，同时满足结构安全性的要求。

3. 家具定制：在定制家具时，了解房间的长、宽、高以及家具的尺寸，可以帮助设计师计算出家具摆放后剩余的空间大小，从而设计出既美观又实用的家居布局。

4. 农业生产：在农业领域，计算农作物的生长空间（如温室大棚的体积）有助于合理安排种植密度，优化光照、通风等条件，提高农作物的产量和品质。

六、总结

通过本文的介绍，我们详细了解了长方体的基本定义、体积的概念以及长方体体积的计算公式和步骤。长方体体积的计算不仅是一个简单的数学运算过程，更是连接理论知识与实际应用的桥梁。掌握这一技能，将有助于我们更好地理解和解决日常生活中的各种问题。希望读者能够通过本文的学习，对长方体体积的计算有一个全面而深入的认识。