揭秘！轻松掌握标准差计算，让你的数据分析更精准

标准差怎么算

在统计学中，标准差是一个极为重要的概念，它用于描述一组数据的离散程度。简单来说，标准差越大，数据越分散；标准差越小，数据越集中。标准差不仅用于单组数据的离散性分析，还可以在多组数据之间进行比较，揭示数据间的相似性或差异性。本文将从多个维度详细解析标准差的计算方法及其应用。

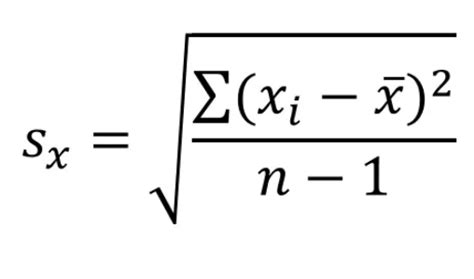
一、标准差的定义

标准差（Standard Deviation），也被称为标准偏差或实验标准差，是衡量数据波动或分散程度的一种量度。在数学上，标准差被定义为数据与其均值（平均值）之差的平方的平均数的平方根。用符号表示即：标准差σ等于方差s²的开平方。

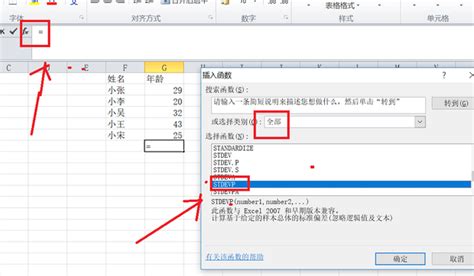
二、标准差的计算公式

标准差的计算有两种基本情况：样本标准差和总体标准差。

1. 样本标准差

当我们从总体中随机抽取一部分数据作为样本进行分析时，使用的标准差计算公式为：

\[

s = \sqrt{\frac{\sum_{i=1}^{n}(x_i - \bar{x})^2}{n-1}}

\]

其中，$s$ 是样本标准差，$n$ 是样本中的数据个数，$x_i$ 是第$i$个数据值，$\bar{x}$ 是样本数据的平均值（算术平均数），即 $\bar{x} = \frac{1}{n}\sum_{i=1}^{n}x_i$。

注意，样本标准差的分母是 $n-1$，这是为了进行无偏估计，即使得通过样本数据计算出的标准差能够更准确地反映总体标准差。

2. 总体标准差

如果我们直接对总体所有数据进行分析，那么使用的标准差计算公式为：

\[

\sigma = \sqrt{\frac{\sum_{i=1}^{N}(x_i - \mu)^2}{N}}

\]

其中，$\sigma$ 是总体标准差，$N$ 是总体中的数据个数，$x_i$ 是第$i$个数据值，$\mu$ 是总体数据的平均值。

在这种情况下，分母为 $N$，因为总体数据已经包含了所有可能的观测值，无需进行无偏估计调整。

三、标准差的应用

标准差在统计学、经济学、金融学、心理学等多个领域都有广泛的应用。以下是一些主要的应用场景：

1. 衡量数据离散程度

标准差最基本的用途就是衡量数据的离散程度。通过计算标准差，我们可以了解数据的波动范围，进而评估数据的稳定性和可靠性。

2. 数据比较

在比较不同数据集时，标准差可以帮助我们判断两组数据的离散程度是否相似。如果两组数据的标准差相近，说明它们的离散程度相似；如果标准差差异较大，则说明它们的离散程度不同。

3. 决策支持

在决策过程中，标准差可以用于评估不同选项的风险。例如，在投资组合管理中，投资者可以使用标准差来衡量不同投资组合的风险水平，从而选择更适合自己风险偏好的投资组合。

4. 质量控制

在工业生产中，标准差常用于质量控制领域。通过设定一定的标准差范围，企业可以监控生产过程中的波动情况，及时发现并纠正异常波动，从而保证产品质量的稳定性。

四、标准差的性质

标准差具有一些重要的性质，这些性质有助于我们更好地理解和应用标准差：

1. 非负性：标准差是非负的，即 $s \geq 0$ 和 $\sigma \geq 0$。

2. 单位：标准差的单位与原数据单位相同。例如，如果原数据是厘米，那么标准差也是厘米。

3. 均值与标准差的关系：标准差与均值呈负相关关系。当均值增大时，如果数据的分布不变，则标准差通常会减小；反之亦然。但需要注意的是，这种关系并不是绝对的，因为标准差还受到数据分布形状的影响。

4. 样本标准差与总体标准差的关系：在大多数情况下，样本标准差会略小于总体标准差。这是因为样本数据只是总体数据的一部分，而总体数据包含了所有可能的观测值。

五、总结

标准差是统计学中一个非常重要的概念，它用于描述数据的离散程度。通过计算标准差，我们可以了解数据的波动范围、评估数据的稳定性和可靠性、比较不同数据集的离散程度以及为决策提供风险支持。无论是样本标准差还是总体标准差，都具有重要的应用价值。在实际应用中，我们需要根据具体的数据情况和分析目的来选择合适的标准差计算公式和分析方法。