揭秘球体体积的神奇计算方法:轻松掌握,让数学不再枯燥!
作者:佚名 来源:未知 时间:2024-10-23
当我们想要了解一个基本而又迷人的几何概念——如何计算球体的体积时,其实这一过程充满了数学的魅力和实用性。球体,作为三维空间中一个完全对称的几何体,其每一个点到球心的距离都相等,这个距离我们称之为球的半径(r)。计算球体的体积,是几何学、物理学以及日常生活中经常会遇到的问题,比如计算篮球、足球的体积,或是了解一个行星、恒星的大致内部空间等。下面,我们就来直接步入正题,了解球体体积的计算方法。
球体体积的计算公式
球体体积的计算依赖于一个简洁而强大的数学公式,即:
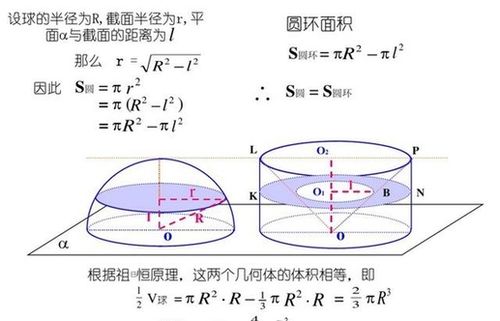
\[ V = \frac{4}{3} \pi r^3 \]
其中,\(V\) 代表球体的体积,\(r\) 是球体的半径,\(\pi\)(Pi)是一个无理数,约等于3.14159...。这个公式揭示了球体体积与其半径的三次方成正比的关系,同时也展现了\(\pi\)这一数学常数在描述圆形和球形几何特性中的核心作用。
如何使用这个公式
要使用这个公式计算球体的体积,你只需要知道球体的半径即可。下面是一个具体的步骤示例:
1. 确定半径:首先,确定你要计算的球体的半径。这个值可以是直接给出的,也可以通过测量或其他方式得到。
2. 代入公式:将已知的半径值代入到球体体积的计算公式中。
3. 计算体积:进行数学运算,得出球体的体积。这里需要注意的是,由于涉及到乘方和\(\pi\)的运算,手动计算可能会比较复杂,建议使用计算器或计算机程序来完成。
实例演示
假设我们有一个半径为5厘米的球体(比如一个小皮球),我们想要知道它的体积是多少。
已知半径 \(r = 5\) 厘米。
代入公式 \(V = \frac{4}{3} \pi r^3\),得到 \(V = \frac{4}{3} \pi \times 5^3\)。
进行计算,\(5^3 = 125\),所以 \(V = \frac{4}{3} \pi \times 125\)。
进一步计算,\(V \approx \frac{4}{3} \times 3.14159 \times 125 = 523.598\) 立方厘米(这里我们取了\(\pi\)的近似值进行计算)。
因此,这个半径为5厘米的球体的体积大约是523.6立方厘米。
背后的数学原理
虽然球体体积的计算公式看起来很简单,但其背后却蕴含了深刻的数学原理。这个公式是通过对球体进行无限次切割,并计算这些小块的总体积来推导出来的。具体来说,它涉及到了微积分中的“极限”和“积分”概念,即通过无限细分和求和来逼近真实的体积值。不过,对于大多数非数学专业的读者来说,了解这一点就足够了,无需深入探究其复杂的数学推导过程。
总结
计算球体的体积是一个既基础又实用的数学技能。通过掌握球体体积的计算公式及其使用方法,我们可以轻松地解决各种与球体体积相关的问题。无论是日常生活中的小物件,还是宇宙中的宏大天体,这个公式都能帮助我们更好地理解和描述它们的空间特性。希望这篇文章能够帮助你更好地掌握这一知识点,享受数学带来的乐趣和便利。
- 上一篇: 想知道'舂'的正确拼音吗?点这里揭晓答案!
- 下一篇: 如何正确书写书信格式?
热门手游
换一换- 精品游戏
- 最热榜单






























