圆台体积求解全攻略：公式、步骤一次搞懂，轻松计算不再难！

在探索几何世界的奇妙之旅中，圆台这一形状以其独特的形态和广泛的应用，总能吸引众多求知者的目光。你是否曾好奇过，那些桥梁的墩柱、建筑物的基座，甚至是精美的台灯底座，它们中许多都蕴含着圆台的形态之美？那么，当我们面对这样一个既实用又美观的几何体时，如何准确计算出它的体积呢？今天，就让我们一起揭开圆台体积计算的神秘面纱，用轻松有趣的方式，走进圆台体积的求解之旅。

圆台初印象

首先，让我们来简单认识一下圆台。圆台，顾名思义，是一个上下底面均为圆形且平行，侧面为曲面的几何体。它看起来就像是一个被“切割”过的圆锥，去掉了顶部尖角后留下的部分。这样的形状不仅稳固，还充满了和谐之美。

公式揭秘：V=1/3πh(r²+R²+rR)

想要计算圆台的体积，我们首先需要掌握一个至关重要的公式：V=1/3πh(r²+R²+rR)。这个公式看起来有些复杂，但别担心，让我们一步步来解析它。

在这个公式中，V代表圆台的体积，π是圆周率（常取值3.14），h是圆台的高，r和R分别是圆台的上底面和下底面的半径。这个公式的背后，其实蕴含着圆锥体积与相似三角形性质的巧妙结合。

圆锥与圆台的渊源

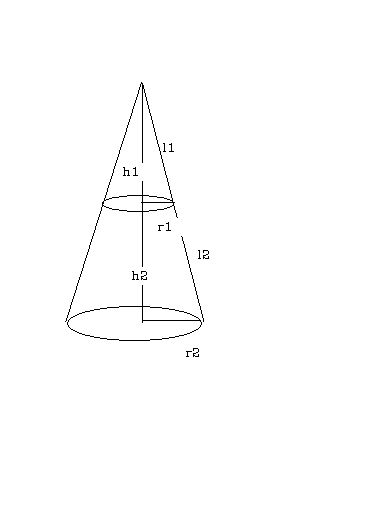
想象一下，如果有一个大圆锥，我们在它的某个高度处水平地“切”一刀，去掉上面的部分，剩下的不就是我们今天要讨论的圆台了吗？这个“切割”的过程，实际上就是圆台体积公式的由来。

假设大圆锥的底面半径为R，高为h1，体积为V1；而我们“切”掉的小圆锥的底面半径为r，高为h2，体积为V2。根据圆锥体积的公式V = 1/3πhr²，我们可以分别求出大圆锥和小圆锥的体积。而圆台的体积V，就是大圆锥的体积V1减去小圆锥的体积V2。

由于圆台的高h等于大圆锥的高h1减去小圆锥的高h2，并且由于相似三角形的性质（即r/R = h2/h1），我们可以通过代数运算和立方差公式的应用，推导出圆台体积的公式V = 1/3πh(R² + Rr + r²)。

实战演练：用公式解决问题

掌握了公式，接下来就是实战演练的时间了。假设我们有一个圆台，其上底面半径为5cm，下底面半径为10cm，高为8cm。想要知道这个圆台的体积有多大吗？

根据圆台的体积计算公式，我们只需将已知数据代入公式中即可：

V = (1/3) * π * 8 * (5² + 10² + 5 * 10)

= (1/3) * 3.14 * 8 * (25 + 100 + 50)

≈ 1464.27 cm³

瞧，通过简单的计算和代入，我们就得到了圆台的体积。这个体积数值不仅是对圆台空间大小的一个量化表示，更是我们理解几何、运用公式解决实际问题的一次成功尝试。

更进一步：圆台的表面积

既然已经掌握了圆台体积的计算方法，不妨再进一步，了解一下圆台表面积的计算。虽然这与体积计算有所不同，但同样充满了数学的魅力和乐趣。

圆台的表面积由三部分组成：上底面积、下底面积和侧面积。侧面积的计算稍微复杂一些，但可以通过微积分或者旋转体表面积公式来求解。不过，为了简化理解，我们可以采用一种近似的方法：将圆台侧面视为由无数个小圆环堆叠而成，然后分别计算这些小圆环的面积并求和。当然，这种方法虽然直观但不够精确，真正的计算还是依赖于微积分或专门的表面积公式。

结语

通过今天的探索，我们不仅学会了如何计算圆台的体积，还初步了解了圆台表面积的计算思路。在这个过程中，我们感受到了数学的严谨与美妙，更体会到了将抽象知识应用于解决实际问题的乐趣。希望这次旅程能够激发你对几何、对数学乃至对整个自然世界的无限好奇与热爱。在未来的日子里，愿你能继续以探索者的姿态，勇往直前，发现更多未知的奥秘。