圆台体积的计算公式详解

在探索几何学的广阔天地中，圆台作为一个独特而重要的几何体，以其独特的形态和广泛的应用吸引着无数学者与爱好者的目光。对于那些对圆台的体积计算感到好奇的朋友们，本文将深入浅出地介绍圆台体积的计算公式，揭示其背后的数学原理与推导过程，旨在帮助大家轻松掌握这一重要知识点。

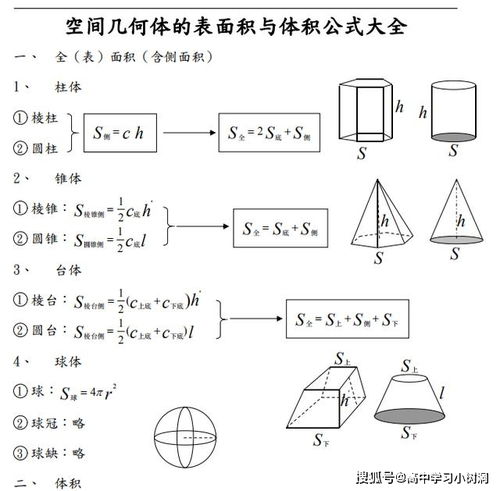
圆台体积公式的奥秘

圆台，顾名思义，是由两个平行且大小不等的圆面（即上底面和下底面）以及连接这两个圆面的侧面所围成的立体图形。其独特的结构使得圆台在计算体积时，需要采用与圆柱、圆锥等简单几何体不同的方法。圆台的体积公式为：

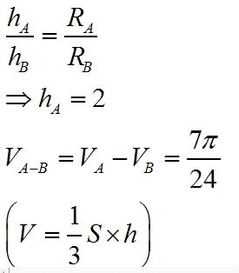
\[ V = \frac{1}{3} \pi h (R^2 + Rr + r^2) \]

其中，\(V\) 代表圆台的体积，\(\pi\) 是圆周率（常取值为3.14），\(h\) 是圆台的高，\(R\) 是下底面的半径，\(r\) 是上底面的半径。这个公式简洁而富有力量，能够精确地计算出任意圆台的体积。

公式推导：从圆锥到圆台

要理解圆台体积公式的由来，我们可以从圆锥入手。想象一个底面半径为\(R\)、高为某个值（不妨设为\(h_1\)）的大圆锥，以及一个底面半径为\(r\)、高为另一个值（设为\(h_2\)）的小圆锥，它们共同构成了圆台的一个“前身”。如果我们从大圆锥中切除小圆锥，剩余的部分就是一个圆台。这里的关键在于，圆台的高\(h\)等于大圆锥的高\(h_1\)减去小圆锥的高\(h_2\)。

利用圆锥体积的公式 \(V = \frac{1}{3} \pi h r^2\)，我们可以分别计算出大圆锥和小圆锥的体积，分别为 \(V_1 = \frac{1}{3} \pi h_1 R^2\) 和 \(V_2 = \frac{1}{3} \pi h_2 r^2\)。由于圆台的体积等于大圆锥体积减去小圆锥体积，即 \(V = V_1 - V_2\)，代入上述公式并整理，我们得到：

\[ V = \frac{1}{3} \pi (h_1 R^2 - h_2 r^2) \]

然而，这还不是最终的圆台体积公式。为了将其转化为与\(h\)、\(R\)、\(r\)直接相关的形式，我们需要利用相似三角形的性质。由于圆台可以看作是由大圆锥和小圆锥通过相似变换得到的，因此有 \(r/R = h_2/h_1\)。解这个比例式，我们可以得到 \(h_2 = rh_1/R\)。将这个结果代入前面的体积差公式，并令 \(h = h_1 - h_2\)，经过一系列代数运算和立方差公式的应用，最终得到圆台的体积公式：

\[ V = \frac{1}{3} \pi h (R^2 + Rr + r^2) \]

实际应用：从理论到实践

掌握了圆台体积的计算公式后，我们就可以将其应用于实际问题的解决中。比如，在建筑设计中，圆台形的结构元素因其独特的力学性能和美观性而受到青睐。了解圆台的体积不仅有助于估算材料用量，还能在成本控制和结构优化方面发挥重要作用。

再如，在工业生产中，圆台形状的容器（如漏斗、某些反应釜等）是常见的设备。计算这些容器的体积，对于工艺设计、生产安排以及安全操作都至关重要。通过应用圆台体积公式，我们可以快速准确地得出所需数据，为生产活动提供有力支持。

总结与展望

圆台体积公式的推导和应用，是几何学与实际应用相结合的一个生动例证。它不仅体现了数学之美——简洁、精确与普适性，还展示了数学在解决实际问题中的巨大威力。随着科技的进步和社会的发展，圆台及其相关几何体的研究将不断深入和拓展，为我们带来更多新的发现和应用。

对于那些对圆台体积公式感到好奇并希望深入了解的朋友们，建议你们亲自动手尝试公式的推导过程，通过实践加深理解。同时，也可以关注几何学领域的前沿动态，探索更多未知的数学世界。相信在未来的学习和探索中，你们会收获更多的知识和乐趣。