揭秘！正方体体积计算公式大公开，你了解吗？

在这个充满几何魅力与实用计算的数字时代，你是否曾被那些复杂而又神秘的数学公式所吸引，尤其是当它们巧妙地解锁自然界与日常生活中的奥秘时？今天，就让我们一起深入探索一个既基础又至关重要的几何概念——正方体体积的计算公式，它不仅是数学殿堂中的一颗璀璨明珠，更是连接理论与实践、抽象与具象的桥梁。

揭秘几何界的“立方体密码”：正方体体积的奥秘

在浩瀚的几何世界里，正方体以其独特的六面等边等角特性，成为了无数科学家、工程师乃至孩子们心中探索的对象。想象一下，从简单的积木游戏到宏伟的建筑设计，正方体的身影无处不在，而掌握其体积的计算方法，则是解锁这些应用背后的关键钥匙。

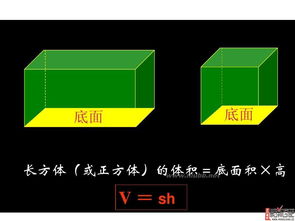
关键词深度融入：正方体、体积、计算公式

当我们谈及“正方体体积的计算公式”，首先映入脑海的是那个简洁而强大的数学表达式：V = a³。这里的“V”代表体积（Volume），“a”则是正方体的边长（Edge Length）。这三个字母，简单却不凡，它们共同编织出了计算正方体体积的魔法咒语。

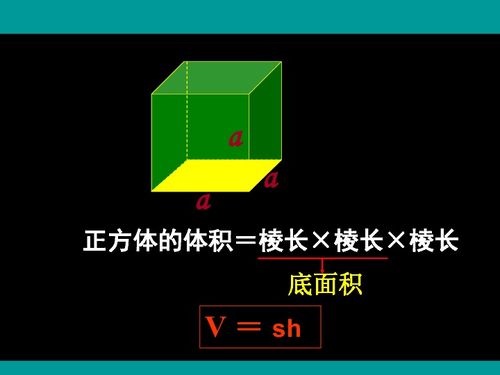
为何它如此重要？

1. 基础教育的里程碑：在初识几何学的旅程中，正方体体积的计算往往是学生们接触到的第一批三维空间概念之一。它不仅帮助学生建立了空间感知能力，还为后续更复杂的几何学习打下了坚实的基础。

2. 实际应用广泛：从日常生活的水箱容量计算，到工业生产的原料需求预估，再到建筑领域的空间规划，正方体体积的计算公式都发挥着不可替代的作用。它如同一把精准的尺子，量化了我们周围的物质世界。

3. 思维训练的利器：通过解决与正方体体积相关的问题，我们不仅能够锻炼数学运算能力，还能培养逻辑思维、空间想象和问题解决等多方面的技能。

深入解析：公式的背后逻辑

那么，这个看似简单的公式背后，隐藏着怎样的数学逻辑呢？想象一下，如果我们把一个正方体沿其长、宽、高三个方向分别切割成若干个小正方体，每个小正方体的边长都是原正方体边长的某个分数。此时，原正方体的体积就等于这些小正方体体积的总和。而由于正方体的特殊性——所有棱长相等，因此每一个小正方体的体积都可以表示为(a/n)³，其中n是切割的份数。但当我们不断增加n的值，直到极限情况（即每个小正方体无限小），那么这些小正方体的数量将趋于无穷大，而它们的总体积则趋近于原正方体的体积V，即V = a³。

实践应用：动手体验计算的魅力

理论虽好，但实践出真知。不妨拿起手边的尺子，测量一个正方体物体的边长，然后代入公式计算其体积。你会发现，这个过程不仅加深了对公式的理解，还让你感受到了数学与现实生活之间的紧密联系。此外，你还可以尝试设计一些基于正方体体积计算的小实验或游戏，与家人朋友一起分享学习的乐趣。

结语：探索不止，学习无界

正方体体积的计算公式，是数学海洋中一朵小小的浪花，但它所蕴含的智慧与美，足以让我们为之倾倒。在这个不断探索与发现的旅程中，让我们保持好奇心，勇于挑战自我，用数学的眼光去审视这个世界，你会发现，原来生活处处皆学问，而数学的魅力，就在于它能够将复杂变得简单，将抽象化为具象。下一次，当你再次遇到与正方体体积相关的问题时，不妨微笑着说：“我已经掌握了这把开启奥秘之门的钥匙。