揭秘！无穷小量等价代换的神奇公式，一学就会

无穷小量等价代换的公式及其应用

在微积分领域中，无穷小量等价代换是一项重要且常用的技巧，它极大地简化了极限的求解过程。本文将围绕“无穷小量等价代换的公式”这一核心概念，从定义、原理、公式列表、应用实例以及注意事项等多个维度进行详细阐述。

一、无穷小量的定义与性质

首先，我们需要明确无穷小量的定义。在极限理论中，若当$x \to x_0$（其中$x_0$可以是任意实数、正无穷大或负无穷大）时，函数$f(x)$趋于0，则称$f(x)$为$x \to x_0$时的无穷小量。特别地，当$x_0 = 0$时，我们通常讨论的是$x \to 0$时的无穷小量。

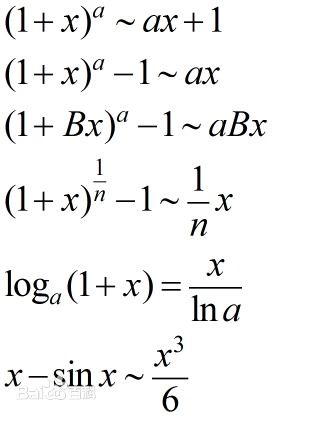
无穷小量具有一些重要性质，如有限个无穷小的和、乘积仍然是无穷小（但无限个不一定）；有界函数与无穷小的乘积仍为无穷小。此外，为了描述不同无穷小趋于0的快慢，引入了无穷小阶的概念。当两个无穷小量之比的极限存在且不为0时，称这两个无穷小为同阶无穷小；若极限为1，则称为等价无穷小。

二、等价无穷小代换的原理

等价无穷小代换的原理基于两个无穷小量之间的等价关系。若$\alpha(x)$和$\beta(x)$是$x \to x_0$时的等价无穷小，即$\lim_{x \to x_0} \frac{\alpha(x)}{\beta(x)} = 1$，则在进行极限运算时，可以用一个无穷小量代替另一个无穷小量，而不改变极限的结果。这一原理基于极限的乘法、除法运算法则。

三、常用的等价无穷小代换公式

在微积分的学习和计算中，掌握一些常用的等价无穷小代换公式是非常必要的。以下是一些在$x \to 0$时常用的等价无穷小代换公式：

1. 三角函数类：

$\sin x \sim x$

$\tan x \sim x$

$\arcsin x \sim x$

$\arctan x \sim x$

$1 - \cos x \sim \frac{x^2}{2}$

2. 指数与对数类：

$e^x - 1 \sim x$

$\ln(1+x) \sim x$

$a^x - 1 \sim x \ln a$（其中$a > 0$且$a \neq 1$）

3. 幂函数类：

$(1+x)^n - 1 \sim nx$（其中$n$为实数）

$\sqrt[n]{1+x} - 1 \sim \frac{x}{n}$（其中$n$为正整数）

4. 复合函数类：

$\tan x - \sin x \sim \frac{x^3}{2}$

这些公式是基于泰勒公式的前几项得到的，因此在$x \to 0$时具有很高的精度。

四、应用实例

为了更好地理解等价无穷小代换的应用，以下给出几个具体的计算实例：

例1：求极限$\lim_{x \to 0} \frac{\sin x}{x}$

根据等价无穷小代换公式，当$x \to 0$时，$\sin x \sim x$，因此：

$$

\lim_{x \to 0} \frac{\sin x}{x} = \lim_{x \to 0} \frac{x}{x} = 1

$$

例2：求极限$\lim_{x \to 0} \frac{e^x - 1 - x}{\sin^2 x}$

首先，利用等价无穷小代换公式，当$x \to 0$时，$e^x - 1 \sim x$，$\sin x \sim x$。于是原式变为：

$$

\lim_{x \to 0} \frac{x - x}{x^2} = \lim_{x \to 0} \frac{0}{x^2} = 0

$$

但这里需要注意，虽然$e^x - 1 \sim x$和$\sin x \sim x$，但在此题中直接使用这两个等价关系并不能直接得出正确结果，因为分母中的$\sin^2 x$是$x^2$的高阶无穷小（即$\sin^2