如何求解两个数的最小公倍数？

在数学的浩瀚宇宙中，最小公倍数（Least Common Multiple, LCM）犹如一座桥梁，连接着数与数之间的共同节奏，它在解决分数运算、时间同步、物品分配等诸多实际问题中扮演着不可或缺的角色。想象一下，你正忙着为班级购买糖果，每位同学对糖果的数量都有特定的要求，如何确保每种糖果的数量都能满足所有同学的需求且尽可能高效？这时，最小公倍数就派上了大用场。下面，我们将直接步入正题，探索如何高效求解两个或多个数的最小公倍数。

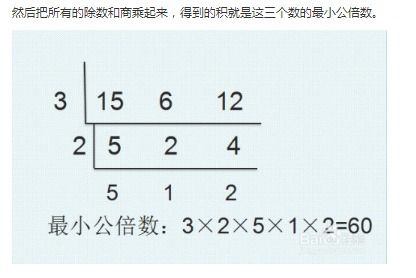
一、基础概念

首先，明确什么是最小公倍数。对于任意两个正整数a和b（不妨设a≤b），它们的最小公倍数是指能够同时被a和b整除的最小的正整数，记作LCM(a, b)。需要注意的是，最小公倍数总是存在的，并且对于任意给定的正整数对，其LCM是唯一的。

二、求两个数的最小公倍数

方法一：列举法（适用于小数）

对于较小的数，可以直接列举出它们的倍数，然后找出第一个共同的倍数。例如，求4和6的最小公倍数，可以列举：

4的倍数：4, 8, 12, 16, ...

6的倍数：6, 12, 18, ...

可见，12是它们第一个共同的倍数，即LCM(4, 6) = 12。

方法二：分解质因数法

对于较大的数，使用分解质因数法更为高效。基本步骤是将每个数分解为质因数的乘积，然后取各质因数的最高次幂相乘，所得结果即为最小公倍数。例如，求LCM(12, 15)：

12 = 2^2 × 3^1

15 = 3^1 × 5^1

取每个质因数的最高次幂相乘：LCM(12, 15) = 2^2 × 3^1 × 5^1 = 60。

方法三：利用最大公约数（GCD）

根据一个重要的数学定理：两个数的乘积等于它们的最大公约数（Greatest Common Divisor, GCD）与最小公倍数的乘积。即，a × b = GCD(a, b) × LCM(a, b)。由此，我们可以推导出：

\[

LCM(a, b) = \frac{a \times b}{GCD(a, b)}

\]

利用这一性质，我们可以先求出两数的最大公约数，然后通过上述公式计算最小公倍数。例如，求LCM(18, 24)：

首先求GCD(18, 24)，由于18=2×3×3，24=2×2×2×3，所以GCD(18, 24) = 2 × 3 = 6；

然后应用公式：LCM(18, 24) = (18 × 24) ÷ 6 = 72。

三、求多个数的最小公倍数

对于多于两个数的情况，我们可以先求前两个数的最小公倍数，然后将结果与第三个数求最小公倍数，以此类推，直至遍历所有数。例如，求LCM(3, 4, 5)：

首先，LCM(3, 4) = 12；

然后，LCM(12, 5) = 60。

所以，LCM(3, 4, 5) = 60。

四、实用技巧与注意事项

1. 优化计算：在实际计算中，特别是面对大数时，合理选择方法至关重要。分解质因数法对于理解最小公倍数的本质很有帮助，但在编程实现时，使用辗转相除法（也称欧几里得算法）求最大公约数，再结合上述公式计算最小公倍数，往往更加高效。

2. 记忆常用数的质因数：对于常见的质数（如2, 3, 5, 7等）及其幂次，保持一定的敏感度可以加快分解质因数的速度。

3. 应用场景联想：将最小公倍数的概念与日常生活或工作中的问题联系起来，比如分配任务、安排时间表等，可以帮助更好地理解和记忆这一知识点。

4. 软件工具辅助：现代科技为我们提供了诸多便捷的计算工具，如计算器应用、编程语言中的库函数等，它们能够快速准确地计算出最小公倍数，是学习和工作中的好帮手。

通过以上介绍，相信你已经掌握了求解最小公倍数的基本方法和技巧。无论是面对简单的数学题目，还是复杂的实际问题，都能灵活运用这一工具，找到最佳的解决方案。在数学探索的旅途中，愿