解锁最小公倍数的奥秘：高效计算方法全攻略

在数学的广阔天地中，求最小公倍数（LCM, Least Common Multiple）是一个基础而重要的概念，它不仅在日常生活中的应用广泛，如分配物资、安排时间表等，更是解决许多数学问题如分数加减、同余方程等的关键步骤。本文将从方法总结的角度出发，系统介绍几种求最小公倍数的高效方法，旨在帮助读者快速掌握并灵活运用这些技巧。

一、概念解析

首先，明确最小公倍数的定义：对于两个或多个整数，它们的最小公倍数是指能够同时被这些整数整除的最小的正整数。例如，对于4和6，它们的最小公倍数是12，因为12既能被4整除，也能被6整除，且是所有这样的数中最小的。

二、常用方法总结

1. 列举法

这是最直观的方法，适用于较小的数。通过列举两个数的公倍数，然后从中找出最小的。例如，求4和6的LCM，可以列举它们的公倍数：4, 8, 12,...，其中最小的是12。此方法虽简单，但效率不高，特别是对于大数时较为繁琐。

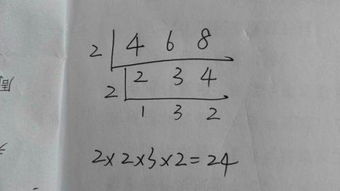
2. 公式法（基于最大公约数）

一个更为高效且广泛使用的方法是利用最大公约数（GCD, Greatest Common Divisor）来求LCM。根据数学原理，两个数的乘积等于它们的最大公约数与最小公倍数的乘积，即：

\[ a \times b = \text{GCD}(a, b) \times \text{LCM}(a, b) \]

由此可得：

\[ \text{LCM}(a, b) = \frac{a \times b}{\text{GCD}(a, b)} \]

利用这一公式，我们可以先通过辗转相除法或更高效的算法求出GCD，再计算出LCM。这种方法对于大数计算尤为有效。

3. 分解质因数法

对于较大的数，分解质因数法也是一种常用的方法。首先，将两个数分别分解为质因数相乘的形式，然后取各质因数的最高次幂相乘，即可得到LCM。例如，对于36和48：

$36 = 2^2 \times 3^2$

$48 = 2^4 \times 3^1$

取各质因数的最高次幂相乘得：

\[ \text{LCM}(36, 48) = 2^4 \times 3^2 = 144 \]

这种方法在理解数的结构方面非常有帮助，同时也适用于多个数的LCM求解。

4. 倍数法（逐步扩大法）

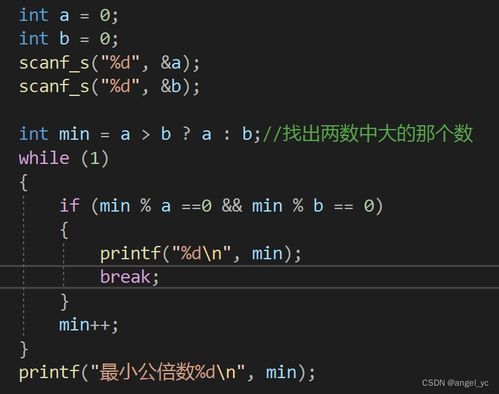
对于某些特定情况，尤其是当两个数相差不大时，可以采用倍数法。具体做法是，从较大的数开始，逐一检查它是否是两个数的公倍数，直到找到最小的那个。虽然这种方法在效率上可能不如其他方法，但在某些特定情境下（如编程实现时考虑可读性）仍有其应用价值。

三、实际应用与拓展

实际应用

分数加减：在进行分数运算时，通常需要找到两个分数的最小公倍数作为通分的分母。

资源分配：在分配有限资源给不同群体时，确保每个群体获得的最小单位数即为LCM，有助于实现公平分配。

时间规划：在安排周期性活动时（如会议、课程等），确定最小公倍数的时间间隔有助于减少冲突，提高效率。

拓展思考

多个数的LCM：上述方法均可推广至求多个数的LCM。对于公式法，可以依次求每两个数的LCM，再将这些结果逐步合并；对于分解质因数法，则是取所有质因数的最高次幂相乘。

算法优化：在计算机科学中，对于大规模数据的处理，求LCM的算法优化尤为重要。比如，利用并行计算、位运算等技术可以显著提高计算效率。

数学竞赛与奥数：在数学竞赛和奥数中，求LCM常常作为考察学生逻辑思维和数学能力的题目出现，熟练掌握这些方法对于提高解题速度和准确率至关重要。

四、结语

求最小公倍数是数学中一个基础而实用的技能，它不仅能够帮助我们解决日常生活中的实际问题，更是深入学习数学其他领域（如数论、代数等）的重要基石。通过本文的介绍，我们系统地总结了求LCM的几种常用方法，并探讨了它们的应用场景和拓展方向。希望读者能够从中受益，不仅学会如何求LCM，更能在实际生活中灵活运用这些数学知识，让数学成为我们探索世界的强大工具。