顶点公式具体是什么?如何应用?
作者:佚名 来源:未知 时间:2024-10-24
在浩瀚的数学海洋中,隐藏着无数令人着迷的公式与定理,它们如同星辰般璀璨,引领着我们探索未知世界的奥秘。今天,让我们一同潜入这片深邃的海域,去揭开一个既神秘又实用的数学宝藏——“顶点公式”的神秘面纱。这不仅仅是一个公式的简单介绍,而是一场关于数学美学与实用性的奇妙之旅。

起点:揭开顶点公式的神秘面纱
想象一下,你正站在一座巍峨的山峰之下,仰望那尖尖的山顶,心中充满了对顶峰美景的向往。在数学的世界里,那些复杂的二次函数图像就如同这一座座山峰,而它们的顶点,正是我们追求的那个“至高点”。顶点公式,就像是那位智慧的向导,引领我们直接找到那座山的最顶端,无需一步步艰难攀登。
深入探索:顶点公式的奥秘
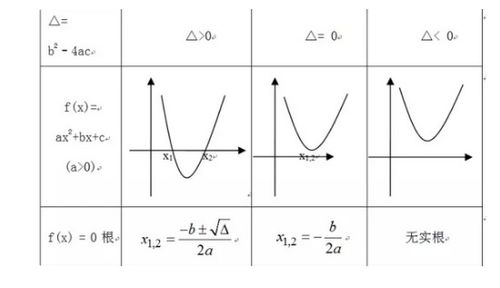
顶点公式,顾名思义,是用来找出二次函数图像顶点坐标的利器。在二次函数的广阔天地里,形如`y = ax^2 + bx + c`(其中`a ≠ 0`)的表达式,描绘了无数或开口向上、或开口向下的抛物线。而每一条这样的抛物线,都拥有一个独一无二的顶点,这个顶点不仅是函数图像的最高点或最低点,也是函数值变化最为微妙的地方。
那么,如何快速准确地找到这个顶点呢?顶点公式便应运而生:
\[
\text{顶点坐标} = \left( -\frac{b}{2a}, c - \frac{b^2}{4a} \right)
\]
这个公式看似复杂,实则蕴含了数学之美。它巧妙地利用了二次函数的系数`a`、`b`和`c`,通过简单的代数运算,直接给出了顶点的横纵坐标。无需繁琐的绘图或逐步代入计算,一键直达目标。
应用实例:生活中的顶点公式
数学并非脱离实际的抽象概念,相反,它无处不在,深深植根于我们的生活之中。顶点公式同样如此,它在多个领域都有着广泛的应用。
1. 物理学中的抛物运动
想象一下,你抛出一个石子,它会沿着一条抛物线轨迹飞行,最终落地。在这个过程中,石子达到的最高点就是抛物线的顶点。如果我们知道石子抛出的初速度和角度,就可以利用物理公式和顶点公式,计算出石子能够达到的最大高度和位置。
2. 经济学中的利润最大化
在经济学中,企业往往追求利润最大化。当产量、成本与销售价格之间呈现二次函数关系时,利用顶点公式可以找到使利润达到最大的生产量。这为企业决策提供了科学的依据,帮助企业在激烈的市场竞争中立于不败之地。
3. 工程设计中的优化问题
在桥梁、建筑等工程设计中,经常需要考虑如何使结构在承受特定载荷时达到最优状态。这时,可以利用顶点公式对设计参数进行优化,找到既能满足安全要求又能节省材料的最佳设计方案。
数学之美:顶点公式的艺术
顶点公式不仅仅是一个实用的工具,它还展现了数学独有的美感。它以一种简洁而优雅的方式,揭示了二次函数图像的本质特征。当我们运用顶点公式解决问题时,就像是在进行一场数学与美的对话,感受着数学世界的和谐与统一。
此外,顶点公式的推导过程也充满了智慧的光芒。它巧妙地利用了配方法或完成平方的技巧,将二次函数转化为顶点式`y = a(x - h)^2 + k`的形式,从而直观地揭示出顶点的位置。这种转化过程不仅锻炼了我们的数学思维能力,也让我们更加深刻地理解了数学中“变与不变”的哲学思想。
结语:与顶点公式共舞
在这个充满未知与挑战的世界里,顶点公式就像是一位忠实的伴侣,陪伴我们穿越数学的迷雾,探寻知识的宝藏。它不仅是解题的钥匙,更是启迪智慧的火花。让我们在未来的学习和生活中,继续与顶点公式共舞,感受数学的魅力与力量吧!
通过这次简短的探索之旅,相信你已经对顶点公式有了更深的理解和认识。记住,数学不是枯燥无味的符号堆砌,而是充满趣味和智慧的奇妙世界。只要我们用心去感受、去发现,就一定能在这个世界中找到属于自己的那份乐趣和成就。
- 上一篇: 揭秘!轻松几步,星立方平台成绩查询全攻略
- 下一篇: 高效发布招聘信息:58同城操作指南






























