想知道基本导数公式大全吗？点击这里，一网打尽所有必知公式！

在探索数学的浩瀚宇宙中，导数作为微积分的核心概念之一，扮演着举足轻重的角色。它不仅连接了函数、极限与变化率，还是解决优化问题、物理运动、经济学模型等多个领域问题的强大工具。对于初涉这一领域的学习者而言，掌握基本导数公式是踏上探索之旅的第一步。本文将带你走进导数公式的世界，逐一揭开那些构筑微积分大厦基石的秘密。

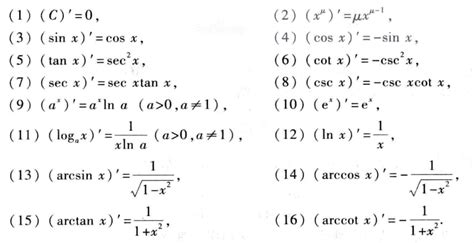
1. 常数与幂函数的导数

常数函数的导数：首先，我们从一个最简单的函数开始——常数函数f(x) = c（其中c为常数）。它的导数为0，这意味着常数函数在其定义域内的任意点都没有变化率。

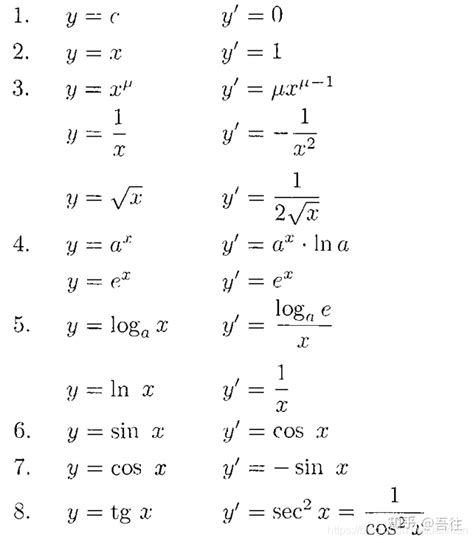
幂函数的导数：接下来，幂函数f(x) = x^n（n为实数）的导数则更为有趣。其导数公式为f'(x) = nx^(n-1)。这个公式揭示了幂函数在求导后的形式变化，特别地，当n=1时，f'(x) = 1，表示线性函数（如f(x) = x）的导数为常数1，反映了其均匀的变化率。

2. 指数与对数函数的导数

指数函数的导数：对于自然指数函数f(x) = e^x（其中e为自然对数的底数，约等于2.71828），其导数公式尤为简洁：f'(x) = e^x。这一性质使得自然指数函数在求解某些复杂导数时变得异常方便，因为它在求导后保持不变，展现出自我相似的特性。

对数函数的导数：与指数函数相对应的，是对数函数。对于自然对数函数f(x) = ln(x)，其导数公式为f'(x) = 1/x（注意x>0）。这反映了对数函数在其定义域内（0,+∞）上随着x的增加而逐渐减小的变化趋势。

3. 三角函数与反三角函数的导数

三角函数的导数：三角函数作为数学中的重要分支，其导数公式同样重要。对于基本的三角函数，如正弦sin(x)、余弦cos(x)和正切tan(x)，其导数分别为：

(sin(x))' = cos(x)

(cos(x))' = -sin(x)

(tan(x))' = (sin(x)/cos(x))' = (cos^2(x) + sin^2(x))/cos^2(x) = 1/cos^2(x) = sec^2(x)（利用了商的导数公式和三角恒等式）

反三角函数的导数：反三角函数，如反正弦arcsin(x)、反余弦arccos(x)和反正切arctan(x)，其导数分别为：

(arcsin(x))' = 1/√(1-x^2)

(arccos(x))' = -1/√(1-x^2)

(arctan(x))' = 1/(1+x^2)

4. 和、差、积、商的导数

和与差的导数：对于任意两个可导函数u(x)和v(x)，它们的和与差的导数遵循线性性质，即：(u(x) ± v(x))' = u'(x) ± v'(x)。

积的导数：乘积的导数则稍微复杂，需要使用乘法法则：(u(x) * v(x))' = u'(x) * v(x) + u(x) * v'(x)。这一法则在解决实际问题时非常有用。

商的导数：商的导数则通过商的导数公式来计算，即：(u(x) / v(x))' = [u'(x) * v(x) - u(x) * v'(x)] / v^2(x)，其中v(x) ≠ 0。

5. 链式法则

链式法则（Chain Rule）是求复合函数导数的重要工具。如果y是u的函数，u又是x的函数，即y = f(u)且u = g(x)，那么y关于x的导数可以通过链式法则求得：(f(g(x)))' = f'(u) * g'(x)。这一法则极大地扩展了我们可以求导的函数类型，使得复杂函数的导数计算成为可能。

结语

至此，我们已经概览了微积分中基本导数公式的核心部分。这些公式不仅是理论学习的基石，更是解决实际问题的有力工具。从简单的常数与幂函数，到复杂的三角函数、反三角函数，再到函数运算（和、差、积、商）的导数，以及