如何快速记忆和差化积公式的口诀是什么？

在这个充满奇妙数学公式的世界里，"和差化积"公式如同一把钥匙，轻轻一转，便能解锁复杂计算中的奥秘，让数字与符号的舞蹈变得优雅而高效。今天，我们就来揭秘这个让无数学生又爱又恨的“魔法公式”，并分享一个让你瞬间牢记、爱不释手的记忆口诀，让学习之路不再枯燥，而是充满趣味与挑战！

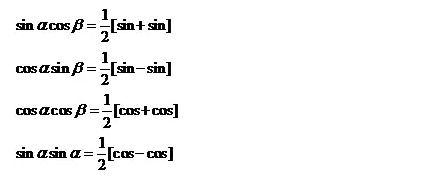
探秘“和差化积”的魔力

在数学的浩瀚星空中，“和差化积”公式犹如一颗璀璨的星辰，它不仅连接了三角函数的基本性质，更是解决许多复杂数学问题的得力助手。简单来说，这个公式能够将两个三角函数的和或差转化为它们的积的形式，从而在特定情境下简化计算过程，提高解题效率。然而，对于初学者而言，这些看似复杂的公式往往令人望而生畏，记忆起来更是难上加难。

记忆口诀：让复杂变得简单

但别担心，这里有一个精心设计的记忆口诀，它将帮助你轻松跨越这道难关，让“和差化积”公式不再是记忆中的拦路虎。准备好了吗？让我们一起念出这段神奇的咒语：

“正加正，正在前；正减正，余弦连；

正加负，正弦变；正减负，余割现。”

这段口诀虽短，却蕴含了“和差化积”公式的精髓，下面我们就来一一解析它的奥秘。

正加正，正在前

这句指的是当两个正弦函数相加时，结果可以表示为两个正弦函数乘积的两倍，再减去一个与它们角度差相关的余弦函数的两倍。具体公式为：

\[ \sin A + \sin B = 2\sin\left(\frac{A+B}{2}\right)\cos\left(\frac{A-B}{2}\right) \]

这里的“正在前”，可以理解为结果中正弦函数出现在前面，引导着整个公式的结构。

正减正，余弦连

当两个正弦函数相减时，情况就有所不同了。此时，结果可以表示为两个余弦函数的乘积的两倍，再减去一个与它们角度和相关的正弦函数的两倍。公式为：

\[ \sin A - \sin B = 2\cos\left(\frac{A+B}{2}\right)\sin\left(\frac{A-B}{2}\right) \]

“余弦连”，形象地描绘了余弦函数在公式中的桥梁作用，连接着两个正弦函数的差。

正加负，正弦变

如果是一个正弦函数与一个余弦函数相加（注意，这里假设余弦函数带有负号），那么结果会涉及到正弦函数的变形。具体来说，它会转化为一个正弦函数与另一个角度的余弦函数的乘积。公式为：

\[ \sin A - \cos B = \sqrt{2}\sin\left(A - \frac{\pi}{4}\right) \]（注意：此公式为简化形式，原“和差化积”不直接包含此形式，但可通过和角公式转换得到类似效果，用于记忆启发）

这里的“正弦变”，意味着在特定条件下，正弦函数会以一种新的面貌出现。

正减负，余割现

最后，当正弦函数减去余弦函数（余弦函数不带负号）时，虽然直接的“和差化积”公式不直接对应此情况，但我们可以借助其他三角函数关系进行转化，或者从记忆口诀的创意角度出发，想象为某种“余割”（非标准术语，仅为记忆辅助）形式的出现，提醒我们这类问题同样可以通过三角函数的变换来解决。

实战演练：让记忆更深刻

理解了口诀之后，不妨找几道相关的练习题来实战演练一番。通过实际应用，你会发现这些公式和口诀是如何在解题过程中发挥作用的。记住，每一次的练习都是对记忆的加深，也是对理解能力的提升。

结语

“和差化积”公式，不再是数学海洋中的一座孤岛，而是你探索未知世界的得力工具。通过这段简单而富有韵律的记忆口诀，我们不仅能够轻松掌握这些公式，还能在解题的过程中感受到数学的魅力与乐趣。记住，学习是一场旅行，而记忆口诀就是那张指引你前行的地图。让我们一起，用智慧和汗水，绘制出属于自己的数学蓝图吧！