揭秘！secx与cscx导数公式的神奇推导，你不可错过的数学奥秘

在数学与物理的广阔领域中，三角函数作为一类重要的数学工具，其导数计算及应用占据着举足轻重的地位。其中，`secx`（正割函数）与`cscx`（余割函数）的导数公式及其推导过程，不仅体现了微积分学的精妙，也揭示了三角函数之间的深刻联系。本文将从多个维度探讨`secx`与`cscx`的导数公式及其推导过程，旨在帮助读者深入理解这些基本概念及其背后的数学原理。

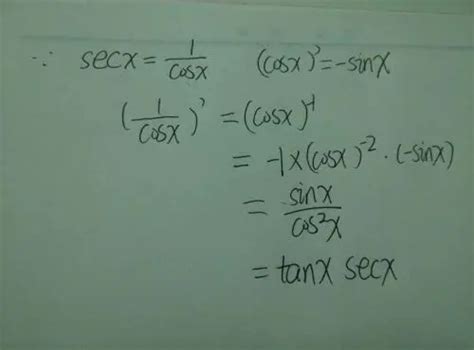
一、`secx`与`cscx`的基本定义

首先，我们回顾一下`secx`与`cscx`的基本定义。在直角三角形中，若角`x`的对边为`a`，邻边为`b`，斜边为`c`，则根据三角函数的定义：

`secx`（正割函数）定义为`c/b`，即斜边与邻边的比，数学表达式为`secx = 1/cosx`。

`cscx`（余割函数）定义为`c/a`，即斜边与对边的比，数学表达式为`cscx = 1/sinx`。

这两个函数在解决与角度、边长相关的问题时具有广泛的应用价值。

二、`secx`导数的推导

接下来，我们详细推导`secx`的导数公式。根据导数的定义，有：

$$ \left( \frac{d}{dx} \sec x \right) = \lim_{{h \to 0}} \frac{\sec(x+h) - \sec x}{h} $$

将`secx`的定义代入上式，得：

$$ \lim_{{h \to 0}} \frac{\frac{1}{\cos(x+h)} - \frac{1}{\cos x}}{h} $$

为了进行化简，我们可以采用通分的方法：

$$ \lim_{{h \to 0}} \frac{\cos x - \cos(x+h)}{h \cos x \cos(x+h)} $$

接下来，利用三角函数的和差化积公式，将上式中的`cos(x+h) - cos x`转化为：

$$ -2\sin\left(\frac{x+h}{2}\right)\sin\left(\frac{h}{2}\right) $$

于是，原式变为：

$$ \lim_{{h \to 0}} \frac{-2\sin\left(\frac{x+h}{2}\right)\sin\left(\frac{h}{2}\right)}{h \cos x \cos(x+h)} $$

进一步化简，利用`sin(θ)/θ`在`θ`趋于0时的极限为1的性质，以及`cos(x+h)`在`h`趋于0时趋近于`cosx`，得：

$$ \frac{-\sin x}{\cos^2 x} = -\tan x \cdot \frac{1}{\cos x} = \tan x \sec x $$

因此，`secx`的导数为：

$$ \left( \frac{d}{dx} \sec x \right) = \sec x \tan x $$

三、`cscx`导数的推导

类似地，我们可以推导`cscx`的导数公式。根据导数的定义，有：

$$ \left( \frac{d}{dx} \csc x \right) = \lim_{{h \to 0}} \frac{\csc(x+h) - \csc x}{h} $$

将`cscx`的定义代入上式，得：

$$ \lim_{{h \to 0}} \frac{\frac{1}{\sin(x+h)} - \frac{1}{\sin x}}{h} $$

同样采用通分的方法，得：

$$ \lim_{{h \to 0}} \frac{\sin x - \sin(x+h)}{h \sin x \sin(x+h)} $$

利用三角函数的和差化积公式，将上式中的`sin x - sin(x+h)`转化为：

$$ 2\cos\left(\frac{2x+h}{2}\right)\sin\left(-\frac{h}{2}\right) $$

注意到`sin(-θ) = -sin θ`，上式可进一步写为：

$$ -2\cos\left(\frac{2x+h}{2}\right)\sin\left(\frac{h}{2}\right) $$

于是，原式变为：

$$ \lim_{{h \to 0}} \frac{-2\cos\left(\frac{2x