揭秘！高中必学向量公式大全，助你轻松掌握向量奥秘

高中向量公式是数学学习中一个既基础又重要的部分，它们不仅为解析几何、物理力学等领域提供了强有力的工具，还深刻体现了数学中的抽象与直观之美。下面，我们就来直接梳理并解释高中阶段常用的几个关键向量公式，帮助大家更好地掌握这一知识点。

1. 向量的加法与减法

公式描述：

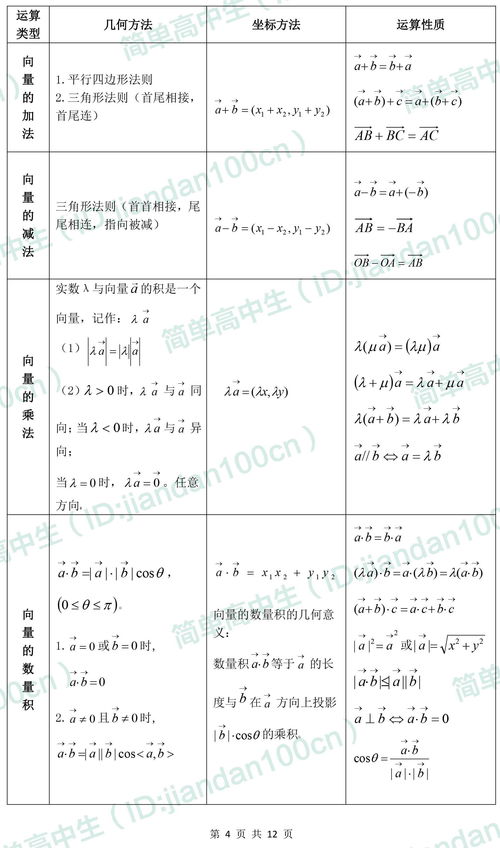
加法：若有两个向量$\vec{a}$和$\vec{b}$，则它们的和$\vec{a} + \vec{b}$是一个新向量，其起点与$\vec{a}$的起点相同，终点与$\vec{b}$以$\vec{a}$的终点为起点的终点相同。

减法：向量$\vec{a}$与$\vec{b}$的差$\vec{a} - \vec{b}$可以看作是$\vec{a}$加上$-\vec{b}$（即$\vec{b}$的反向向量），结果向量的起点与$\vec{a}$的起点相同，终点由$\vec{a}$的终点沿$-\vec{b}$方向移动$|\vec{b}|$的距离得到。

几何意义：向量加法与减法在几何上表现为平行四边形的对角线或三角形法则。

2. 向量的数乘

公式：设实数$\lambda$与向量$\vec{a}$，则它们的数乘（标量乘法）为$\lambda\vec{a}$，其模长为$|\lambda||\vec{a}|$，方向当$\lambda > 0$时与$\vec{a}$相同，当$\lambda < 0$时与$\vec{a}$相反。

几何意义：数乘改变了向量的长度（或称为模）和/或方向，但不改变向量的方向性（除非乘以负数）。

3. 向量的点积（数量积）

公式：对于两个向量$\vec{a} = (a_1, a_2)$和$\vec{b} = (b_1, b_2)$，它们的点积定义为$\vec{a} \cdot \vec{b} = a_1b_1 + a_2b_2$。

几何意义：

点积的结果是一个标量，而非向量。

$\vec{a} \cdot \vec{b} = |\vec{a}| \cdot |\vec{b}| \cdot \cos\theta$，其中$\theta$是两向量之间的夹角。这揭示了向量间夹角与它们长度乘积及点积之间的关系。

当两向量垂直时，$\theta = 90^\circ$，$\cos 90^\circ = 0$，因此$\vec{a} \cdot \vec{b} = 0$。

4. 向量的模长（长度）

公式：对于二维向量$\vec{a} = (a_1, a_2)$，其模长（或长度）为$|\vec{a}| = \sqrt{a_1^2 + a_2^2}$。

几何意义：模长表示向量在空间中从原点到其终点的直线距离。

5. 向量的方向角与单位向量

方向角：向量与坐标轴正方向所成的角称为该向量的方向角。对于二维向量，通常考虑与x轴正方向的角度。

单位向量：模长为1的向量称为单位向量。任意非零向量$\vec{a}$都可以表示为$\vec{a} = |\vec{a}|\vec{u}$，其中$\vec{u}$是与$\vec{a}$同向的单位向量。

6. 向量的共线（平行）与垂直

共线（平行）：两向量$\vec{a}$与$\vec{b}$共线（或平行）当且仅当存在一个非零实数$\lambda$，使得$\vec{a} = \lambda\vec{b}$。

垂直：两向量$\vec{a}$与$\vec{b}$垂直当且仅当它们的点积为0，即$\vec{a} \cdot \vec{b} = 0$。

7. 向量的分解

任何向量都可以分解为两个或多个已知方向上的分量之和。例如，在二维坐标系中，向量$\vec{a}$可以分解为x轴和y轴方向上的分量，即$\vec{a} = a_1\vec{i} + a_2\vec{j}$，其中$\vec{i}$和$\vec{j}$分别是x轴和y轴方向上的单位向量。