如何轻松计算线性回归线斜率?掌握SLOPE函数,一步到位!
作者:佚名 来源:未知 时间:2024-10-27
在数据探索与分析的浩瀚宇宙中,每一个函数都像是璀璨星辰,引领着我们穿越数据迷雾,寻找隐藏于数字背后的真相。今天,我们要深入探索的,是一颗尤为耀眼的星辰——SLOPE函数,它虽在名字上略显低调,实则扮演着计算线性回归线斜率这一关键角色的“幕后英雄”。想象一下,当你手握一堆散乱的数据点,渴望从中抽丝剥茧,找到那条能够揭示数据间关系的直线时,SLOPE函数就如同你的魔法棒,轻轻一挥,便能让一切变得清晰起来。
线性回归的魅力:从混沌到秩序
在数据的海洋里,线性回归模型如同一座灯塔,为我们照亮了前行的道路。它以一种简洁而强大的方式,描述了两个或多个变量之间的线性关系。简单来说,当你发现某个变量的变化似乎与另一个变量以某种恒定的速率同步增减时,线性回归就派上了用场。比如,预测房屋价格随面积增大的变化趋势,或者分析广告投入与销售额增长的关系,线性回归都是不可或缺的工具。
SLOPE函数:斜率背后的智慧
在众多计算线性回归参数的方法中,SLOPE函数以其直接、高效的特性脱颖而出。不同于一些复杂的统计软件包或编程语言中的内置函数,SLOPE(有时也被称为SLOPE函数,尽管具体命名可能因软件而异,但核心功能相同)专注于一个核心任务:计算线性回归线的斜率。斜率,作为线性回归模型的核心参数之一,不仅揭示了自变量(X)每变化一个单位时,因变量(Y)平均变化多少,还是评估变量间关联强度与方向的重要指标。
实战演练:SLOPE函数的魅力展现
为了更直观地理解SLOPE函数的工作原理,让我们通过一个简单的例子来演示。假设你手中有这样一组数据,记录了某地区不同月份的平均气温(X)与该月冰淇淋销售量(Y)的关系。你的目标是找出这两者之间的线性关系,并计算出回归线的斜率。
1. 数据准备:首先,你需要将数据整理成两列,一列是月份平均气温(X),另一列是对应月份的冰淇淋销售量(Y)。
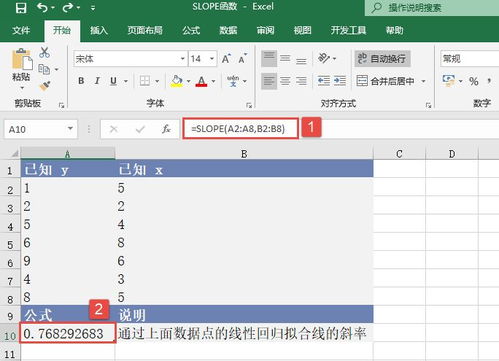
2. 应用SLOPE函数:接下来,利用你的数据分析工具(如Excel、R、Python等)中的SLOPE函数,指定X和Y的范围作为函数的输入参数。在Excel中,你可能需要输入类似`=SLOPE(Y范围, X范围)`的公式;而在R或Python中,虽然具体的函数调用方式可能有所不同,但核心理念相同——都是基于给定的X和Y值计算斜率。
3. 解读结果:SLOPE函数会返回一个数值,即线性回归线的斜率。如果斜率为正,表示随着气温的升高,冰淇淋销售量也在增加;如果斜率为负,则意味着气温升高反而导致销售量下降(尽管这在现实情境中不太常见,但理论上是有可能的)。斜率的绝对值越大,说明两者之间的线性关系越强。
SLOPE函数之外的探索
值得注意的是,虽然SLOPE函数为我们提供了计算斜率的便捷途径,但在实际应用中,线性回归模型往往涉及更多参数和考量。除了斜率外,截距(intercept)也是线性方程的重要组成部分,它表示当自变量为0时,因变量的预测值。此外,为了更好地评估模型的拟合优度,我们还需要计算决定系数(R²)、标准误差等统计量。
此外,当数据不满足线性回归的基本假设(如线性关系、误差项的正态性、同方差性等)时,简单使用SLOPE函数可能无法得到准确或有效的结果。此时,可能需要考虑使用其他更复杂的回归模型,如多项式回归、逻辑回归或岭回归等。
结语
综上所述,SLOPE函数作为计算线性回归线斜率的得力工具,在数据分析与建模中发挥着不可或缺的作用。它不仅帮助我们揭示了变量间的线性关系,还为我们进一步的数据探索和决策制定提供了坚实的基础。然而,正如所有强大的工具一样,正确理解和恰当使用SLOPE函数同样重要。只有这样,我们才能在数据的海洋中乘风破浪,找到那些真正有价值的信息和洞见。
- 上一篇: 如何有效克服害羞心理,自信面对日常挑战?
- 下一篇: 解锁孩子害羞情绪的秘诀:家长必看的高效应对策略






























