求解！15度角对应的三角函数值是多少？

当我们深入探索数学的广袤领域时，三角函数作为连接几何与代数的桥梁，扮演着举足轻重的角色。其中，特定角度如15度的三角函数值，不仅是理论学习中的基础知识点，也是解决实际应用问题时的关键工具。本文将围绕“15度三角函数值是什么”这一主题，详细阐述15度角下正弦、余弦和正切函数的计算方法及其含义。

引言

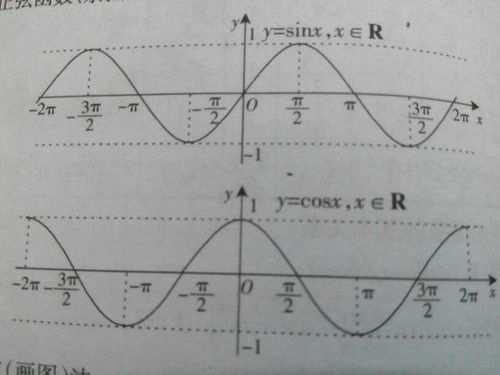
三角函数，顾名思义，是角的函数，它们在直角三角形中定义，并可通过单位圆上的点来更一般地理解。正弦（sin）、余弦（cos）和正切（tan）是三角函数中最基本也是最重要的三种。对于特定的角度，如15度，这些函数的值具有特定的数学意义和实际应用价值。

15度三角函数值的计算方法

利用特殊角的三角函数值推导

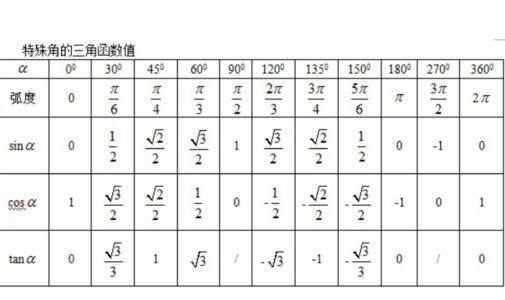
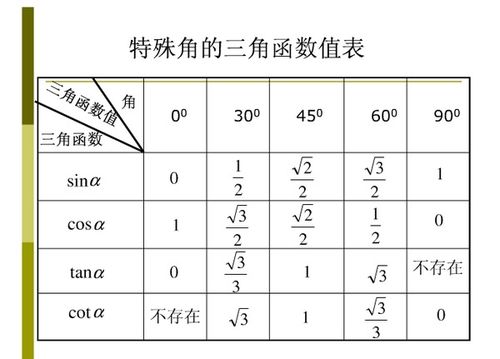
由于直接计算15度角的三角函数值可能较为复杂，我们可以借助已知的30度和45度（或60度，取决于采用哪种标准角度划分）等特殊角的三角函数值，通过角度加减公式或倍角公式来间接求解。

例如，利用正弦的两角差公式：

$$\sin(A - B) = \sin A \cos B - \cos A \sin B$$

我们可以将15度视为45度与30度的差，即：

$$\sin 15^\circ = \sin(45^\circ - 30^\circ) = \sin 45^\circ \cos 30^\circ - \cos 45^\circ \sin 30^\circ$$

代入已知值：

$$\sin 45^\circ = \frac{\sqrt{2}}{2}, \quad \cos 30^\circ = \frac{\sqrt{3}}{2}, \quad \cos 45^\circ = \frac{\sqrt{2}}{2}, \quad \sin 30^\circ = \frac{1}{2}$$

得到：

$$\sin 15^\circ = \frac{\sqrt{2}}{2} \times \frac{\sqrt{3}}{2} - \frac{\sqrt{2}}{2} \times \frac{1}{2} = \frac{\sqrt{6} - \sqrt{2}}{4}$$

类似地，对于余弦和正切，我们也可以利用相应的角度加减公式或倍角公式进行计算，但这里为了简洁，不再逐一展开。

借助单位圆

另一种直观理解并计算15度三角函数值的方法是使用单位圆。在单位圆上，任何角度α对应的正弦值等于该角度终边与单位圆交点的y坐标，余弦值等于x坐标，正切值则为y坐标与x坐标的比值。虽然直接通过单位圆上的点确定15度角的坐标较为复杂，但这种方法为我们提供了一种几何直观，有助于深入理解三角函数。

15度三角函数值的实际应用

尽管15度这个角度在日常生活中不如30度、45度或60度那样常见，但其三角函数值在计算、物理、工程等多个领域仍有广泛应用。例如，在解决与角度、距离和高度相关的实际问题时，经常需要利用三角函数的性质进行转化和计算。掌握15度（及其他任意角度）的三角函数值，对于提高问题解决能力和数学素养具有重要意义。

结论

综上所述，15度三角函数值作为数学领域中的基础知识，不仅具有丰富的数学内涵，还具备广泛的实用价值。通过特殊角的三角函数值推导、单位圆的应用等方法，我们可以有效地求解出15度角的正弦、余弦和正切值。这些值的掌握，不仅有助于我们深入理解三角函数的本质和性质，也为我们在解决实际问题时提供了有力的数学工具。因此，在学习和实践中，我们应给予足够的重视和关注。