圆锥的表面积与底面积详解
作者:佚名 来源:未知 时间:2024-10-29
圆锥,这一几何形体,在我们的日常生活中或许不如圆形、正方形那样常见,但在建筑学、工程学乃至自然界的某些现象中,它都扮演着不可或缺的角色。那么,当我们谈及“圆锥面积是什么呢?”这一问题时,实际上是在探索圆锥这一立体图形表面覆盖的平面区域的大小。
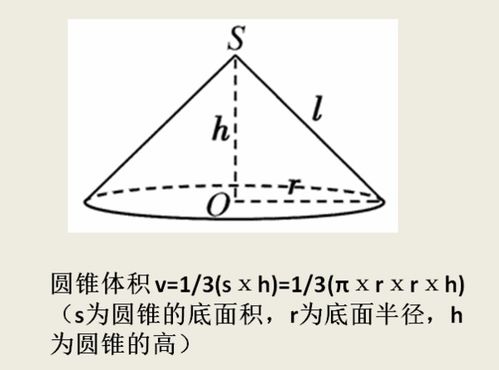
首先,要明确的是,圆锥并非一个简单的平面图形,而是一个三维立体,由一个圆形底面、一个顶点以及连接顶点和底面圆周上每一点的侧面所组成。因此,当我们谈论圆锥的“面积”时,实际上包含了两个主要部分:底面积和侧面积。
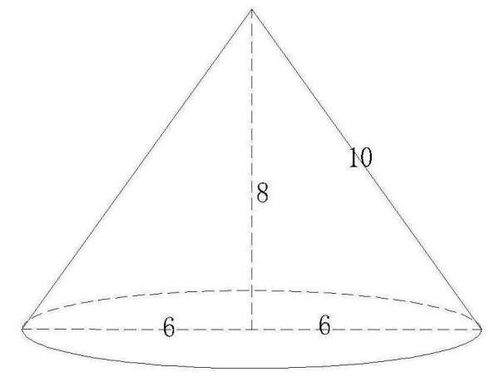
圆锥的底面积
圆锥的底面积,顾名思义,就是其底部圆形的面积。根据圆的面积计算公式,我们知道圆的面积A等于π(圆周率,约等于3.14159)乘以半径r的平方,即A = πr²。这里的半径r,是从圆锥的底面圆心到圆上任意一点的距离。因此,只要知道了圆锥底面的半径,就可以直接应用这个公式来计算出圆锥的底面积。
圆锥的侧面积
相较于底面积的直接计算,圆锥的侧面积计算稍微复杂一些。圆锥的侧面是一个曲面,展开后类似于一个扇形。为了计算这个曲面的面积,我们需要用到扇形面积的计算公式,并结合圆锥的几何特性进行推导。
圆锥的侧面展开后,扇形的弧长等于圆锥底面的周长,即2πr。而扇形的半径,在这里被称为圆锥的母线,是从圆锥的顶点到底面圆周上任意一点的线段。我们设这个母线的长度为l。
扇形面积的计算公式是:面积 = (弧长/360°) × π × 扇形半径²。但在这里,因为圆锥侧面展开后的扇形是圆的一部分,且这一部分的弧长就是整个圆的周长,所以我们可以用一个简化的形式来表示:侧面积 = (弧长) × (扇形半径) / 2 = 2πr × l / 2 = πrl。
圆锥的全面积
综合以上两部分,圆锥的全面积即为底面积与侧面积之和。将之前计算得到的底面积A = πr²和侧面积πrl相加,我们得到圆锥的全面积公式为:A_total = πr² + πrl。
这个公式简洁而全面地表达了圆锥表面积的计算方法,无论是对于数学学习中的理解,还是在实际工程或设计中的应用,都具有重要意义。
实际应用中的考量
在实际应用中,了解圆锥的面积不仅有助于我们进行几何计算,还能在多种场景下发挥作用。比如,在建筑设计中,圆锥形的屋顶结构需要精确计算其表面积以确定所需的材料量;在水利工程中,圆锥形的蓄水池或排水管道的设计同样需要考虑其表面积,以评估其建造成本和维护难度;而在自然科学领域,某些呈圆锥形的自然结构(如火山锥)的研究,也离不开对其表面积的准确测量和分析。
总之,“圆锥面积是什么呢?”这一问题,实际上引领我们进入了一个关于三维几何形态、数学计算以及实际应用的广阔领域。通过理解和掌握圆锥面积的计算方法,我们不仅能够提升在数学学科上的素养,还能在更广泛的领域中发挥这些知识的价值。
- 上一篇: 《骆驼祥子》的作者是谁?
- 下一篇: 如何通过收件人手机号查询邮政快递信息?






























