想知道平方怎么轻松算吗?一键解锁计算方法!
作者:佚名 来源:未知 时间:2024-10-30
在日常生活中,计算平方是一项基础且频繁使用的数学技能,它不仅局限于学校课堂,更渗透到了科学探索、工程计算、金融投资、乃至日常生活的方方面面。平方,简单来说,就是一个数自乘的结果,即a的平方等于a乘以a(表示为a²或a^2)。虽然这个概念看似简单,但其背后的逻辑和应用却丰富多彩。下面,我们就从几个不同的维度来深入探讨“平方怎么算”及其广泛应用。
一、数学基础:平方的概念与性质
定义与表示:如前所述,平方是指一个数与其自身的乘积。在数学中,平方常用符号“²”或“^2”来表示。例如,5的平方写作5²或5^2,计算结果为25。
性质:平方具有一些重要的数学性质,如非负性(任何实数的平方都是非负的)、平方根的存在性(除了0以外的任何正数的平方都有两个平方根,一个正的和一个负的,但习惯上我们只说非负的那个)、以及平方的乘法分配律等。
二、计算方法:手算与工具辅助
手算方法:对于较小的数,我们可以直接通过乘法来计算其平方。例如,计算7的平方,就是7乘以7,得到49。此外,还有一些技巧可以简化计算过程,如利用差平方公式(a²-b²=(a+b)(a-b))的逆用、完全平方公式等。
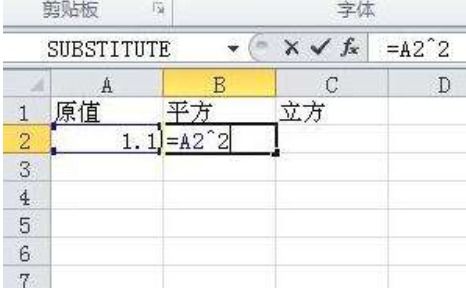
工具辅助:随着科技的发展,计算器、智能手机、计算机等电子设备成为了我们计算平方的强大工具。只需输入相应的数值,选择平方运算,即可迅速得到结果。此外,许多编程语言和数学软件也提供了计算平方的函数,极大地方便了科学研究和工程计算。
三、几何意义:面积与图形的关联
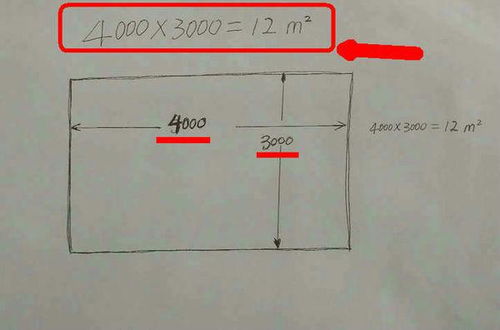
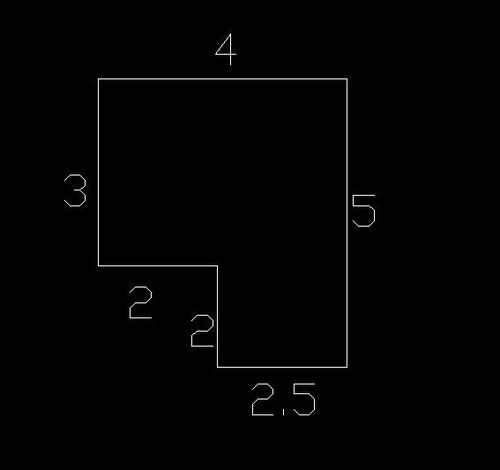
平方在几何学中有着直观且深刻的意义。它代表了一个二维平面图形(如正方形、矩形等)的面积。例如,一个边长为a的正方形的面积就是a²。这种关联不仅加深了我们对平方概念的理解,还使得平方计算在测量、建筑设计、地理测绘等领域发挥着重要作用。
四、物理应用:速度、加速度与力的计算
在物理学中,平方的概念无处不在。速度的平方(v²)与动能(K)直接相关,根据动能公式K=1/2mv²(m为质量),我们可以知道物体的动能与其速度的平方成正比。同样,加速度(a)的计算在动力学中也非常重要,而加速度的表达式(如牛顿第二定律F=ma)中,虽然直接未涉及平方,但加速度的效果(如冲量、位移等)的计算往往与时间的平方或速度的平方相关。此外,在力的合成与分解中,利用勾股定理(c²=a²+b²)可以计算直角三角形的斜边长度,这在力学分析中尤为关键。
五、经济金融:复利与投资回报
在经济和金融领域,平方的概念与复利计算紧密相连。复利是指利息在计算时,不仅考虑本金,还将之前累计的利息纳入基数中。在复利计算公式中,时间的平方项(虽然不是直接出现,但通过连续复利公式推导可得出与时间相关的指数增长效应)体现了时间对投资回报的巨大影响。简单来说,随着时间的推移,复利效应会使得投资回报以惊人的速度增长,这正是平方(或更广义的指数增长)在经济领域中的一个典型应用。
六、信息技术:算法设计与性能优化
在信息技术领域,平方运算也是许多算法和数据处理过程中的关键步骤。例如,在信号处理中,功率谱密度的计算就涉及到平方运算;在图像处理中,亮度、对比度调整等操作也可能涉及到像素值的平方变换。此外,在算法设计中,如何高效地计算平方(特别是在大数据量和高计算复杂度的情况下)成为了一个重要的研究课题。通过利用数学性质、优化算法结构、利用并行计算等技术手段,可以显著提升平方运算的效率,从而加快整体数据处理的速度。
结语
综上所述,平方作为数学中的一个基本概念,不仅在数学本身有着丰富的性质和应用,还广泛渗透到了物理、经济、信息技术等多个领域。从基础的数学计算到复杂的科学计算,从日常生活的点滴到高科技的前沿探索,平方都在默默地发挥着它的作用。因此,掌握平方的计算方法及其应用不仅是我们学习数学的基本要求,更是我们理解和改变世界的重要工具。