问答揭秘：如何计算两点及点与线之间的精确距离公式？

在几何学与数学分析领域，两点之间的距离公式以及点与线之间的距离公式是极其重要且基础的概念。它们不仅是解决几何问题的基础工具，也广泛应用于物理、工程等多个领域。本文将从多个维度详细探讨这两类公式的推导、应用及理解。

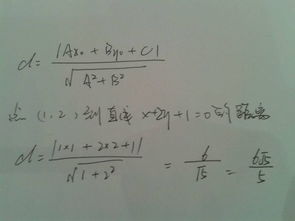
两点之间的距离公式

公式定义

两点间距离公式是描述平面上两个点之间直线距离的数学表达式。设两点A(x₁, y₁)和B(x₂, y₂)，则A、B两点之间的距离d可以通过以下公式计算：

\[d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\]

这个公式直观地反映了两点间距离的几何意义，即两点构成的线段的长度。

公式推导

两点间距离公式的推导可以基于勾股定理。我们可以想象过点A做一条与x轴平行的直线，过点B做一条与y轴平行的直线，这两条直线的交点为C。由于x轴与y轴垂直，因此AC垂直于BC，从而构成了一个直角三角形ACB。在这个三角形中，直角边AC的长度为|x₂ - x₁|，直角边BC的长度为|y₂ - y₁|，而斜边AB的长度即为两点间的距离d。根据勾股定理，有：

\[AB^2 = AC^2 + BC^2\]

代入AC和BC的长度，即得：

\[d^2 = (x_2 - x_1)^2 + (y_2 - y_1)^2\]

对两边开方，即得两点间距离公式。

应用实例

两点间距离公式在解决实际问题时有着广泛的应用。例如，在地图上计算两个城市之间的直线距离、在物理学中计算物体运动的实际路径长度、在工程领域计算两点之间的最短路径等。

点与线之间的距离公式

公式定义

点与线之间的距离公式是描述平面上一个点到一条直线之间最短距离（即垂线距离）的数学表达式。设直线L的方程为Ax + By + C = 0，点P的坐标为(x₀, y₀)，则点P到直线L的距离d可以通过以下公式计算：

\[d = \frac{|Ax_0 + By_0 + C|}{\sqrt{A^2 + B^2}}\]

这个公式表示了点P到直线L的垂线段的长度。

公式推导

点与线之间距离公式的推导需要用到点到直线的垂线性质以及代数运算。首先，我们设点P到直线L的垂线为l'，垂足为Q。由于l'是垂直于直线L的，因此l'的斜率与直线L的斜率互为负倒数。但在此处，我们不需要直接求出l'的方程，而是可以通过联立直线L和l'的方程来找到垂足Q的坐标。然而，这种方法较为繁琐。更简洁的方法是直接利用点到直线的距离公式进行推导。

具体地，我们可以将点到直线的距离定义为从点P向直线L做垂线，垂足为Q，则PQ的长度即为所求的距离。根据点到直线的距离定义，我们可以利用直线的标准方程和点到直线的垂线性质，通过代数运算得到上述公式。

应用实例

点与线之间的距离公式同样在多个领域有着广泛的应用。例如，在地理信息系统中计算某一点到道路、河流等线性要素的最短距离；在物理学中计算粒子到电场线或磁场线的最近距离；在工程设计中计算建筑物到道路或河流的安全距离等。

深入理解

公式对称性

在两点间距离公式中，点的位置是对称的，即(x₁, y₁)和(x₂, y₂)可以互换而不影响结果的正确性。这反映了距离的无方向性。同样地，在点与线之间的距离公式中，虽然点P的坐标和直线L的方程是固定的，但公式本身也体现了某种对称性——即点到直线的距离是唯一的，不受观察角度或坐标系统选择的影响。

几何与代数的结合

两点间距离公式和点与线之间的距离公式不仅是几何学的产物，更是代数与几何相结合的典范。这些公式的推导过程中涉及到了勾股定理、直线的标准方程、点到直线的垂线性质等几何概念，同时也需要用到代数运算和方程求解等代数技巧。这种结合使得我们能够用更加精确和量化的方式来描述和分析几何问题。

结语

两点之间的距离公式及点与线之间的距离公式是几何学中的基础工具，它们不仅在理论上具有重要意义，更在实际应用中发挥着不可替代的作用。通过深入理解这些公式的推导过程和应用实例，我们可以