如何区分分子和分母?
作者:佚名 来源:未知 时间:2024-10-31
在我们日常的数学学习和生活中,分数是一个既常见又重要的概念。无论是计算、测量还是解决实际问题,分数都扮演着举足轻重的角色。然而,对于初学者来说,分数中的分子和分母往往容易混淆,使得他们在理解和运用分数时感到困惑。那么,分子和分母究竟应该怎么区分呢?本文将详细讲解分子和分母的概念、区别以及它们在实际中的应用,帮助大家轻松掌握这一基础而关键的知识点。
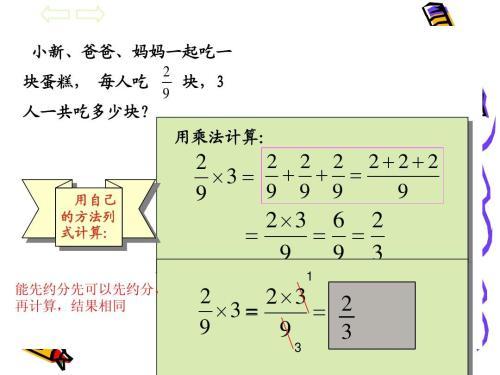
首先,让我们从定义入手。分数是表示一个数(通常称为被除数)除以另一个数(通常称为除数)的结果。在分数中,上面的数字被称为分子,它代表被除数;而下面的数字被称为分母,它代表除数。因此,一个分数的基本形式可以表示为“分子/分母”。例如,在分数3/4中,3是分子,4是分母。

接下来,我们深入探讨分子和分母的区别。

1. 位置不同:这是分子和分母最直观的区别。在分数中,分子总是位于上面,而分母总是位于下面。这种位置关系使得我们可以一目了然地识别出分子和分母。
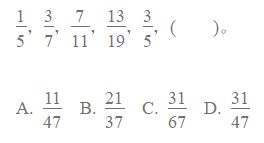
2. 代表意义不同:分子和分母不仅位置不同,它们所代表的意义也截然不同。分子代表被除数,即我们想要分割或测量的总量;而分母代表除数,即我们将总量分割成的等份数量。因此,分子决定了我们有多少东西可以分配,而分母决定了我们将这些东西分成多少份。
3. 影响分数的值:分子和分母的变化会直接影响分数的值。例如,在分数3/4中,如果我们保持分母不变而增加分子(例如变为6/4),分数的值就会增大;相反,如果我们保持分子不变而增加分母(例如变为3/8),分数的值就会减小。这种变化关系反映了分子和分母在分数中的相对重要性。
4. 计算规则不同:在进行分数的加减乘除运算时,分子和分母遵循不同的计算规则。例如,在加法中,我们需要找到两个分数的最小公倍数作为通分母,然后将分子相加;在乘法中,我们只需将两个分数的分子相乘并将两个分母相乘即可得到结果。这些计算规则使得我们能够准确地处理分数问题。
现在,让我们通过一些具体的例子来进一步理解分子和分母的区别。
假设我们有一个披萨,想要将它均匀地分给4个人。在这种情况下,披萨可以被视为总量(即分子),而人数则代表除数(即分母)。因此,每个人分得的披萨份额可以表示为1/4,其中1是分子(代表披萨这个总量被分割成的一份),4是分母(代表有4个人需要分配披萨)。
再比如,如果我们想要计算一个长方形花园的面积,并且知道它的长是5米,宽是3米。那么,面积可以表示为5×3=15平方米。如果我们想将这个面积表示为分数形式(例如为了进行比例计算),我们可以将其写为15/1,其中15是分子(代表面积总量),1是分母(在这里代表一个单位面积或基准)。当然,在实际应用中,我们通常会省略分母为1的分数形式,直接称其为整数或小数。
此外,分子和分母在分数运算中也扮演着重要角色。例如,在进行分数的乘法运算时,我们需要将两个分数的分子相乘并将两个分母相乘来得到结果。这种运算规则确保了我们在处理分数时能够保持数学上的一致性。同样地,在进行分数的除法运算时,我们可以将其转化为乘法运算(即乘以除数的倒数),然后应用相同的规则来计算结果。
除了基本的运算外,分子和分母还在分数的其他应用中发挥着关键作用。例如,在比较分数的大小时,我们需要比较它们的分子和分母来确定哪个分数更大或更小。这通常涉及将分数转换为具有相同分母的形式(即找公分母)以便进行比较。同样地,在求解分数方程时,我们可能需要对方程进行变形或运算以消除分数形式并找到解。在这些过程中,正确区分和理解分子和分母是至关重要的。
总之,分子和分母是分数中的两个关键组成部分它们不仅位置不同、代表意义不同而且在分数的值、计算规则以及实际应用中都发挥着重要作用。通过本文的讲解和示例分析相信大家对分子和分母的区别有了更清晰的认识。在未来的数学学习和生活中希望大家能够运用这些知识来更好地理解和处理分数问题。
最后需要注意的是虽然分子和分母在分数中扮演着重要角色但在实际应用中我们也需要注意它们的取值范围和限制条件。例如在某些情况下分母不能为零否则分数将变得无意义或产生无穷大的结果。因此在进行分数运算或应用时需要仔细审查题目条件和要求以确保结果的准确性和合理性。
- 上一篇: 车厘子保鲜秘籍:让美味持久留存
- 下一篇: 轻松步骤教你如何开通分付






























