揭秘：分子与分母，数学世界的构建基石

在数学领域中，分数是一个基础而重要的概念，它用于表示整体被等分为若干部分后，取出的部分与整体之间的关系。当我们谈论分数时，两个核心组成部分不可避免地跃然纸上——分子与分母。这两个术语，虽简短却蕴含深意，共同构成了分数的骨架，使其能够精准地传达数量的比例关系。接下来，就让我们深入探究，以简洁明了的语言，揭示分子与分母的本质。

首先，让我们从分数的构成说起。一个标准的分数形式可以写作a/b（其中a、b均为整数，且b≠0），这里的a便是我们通常所说的分子，而b则是分母。分子位于分数线的上方，分母则位于其下方，这一位置关系直观地反映了它们在分数中所扮演的角色和重要性。

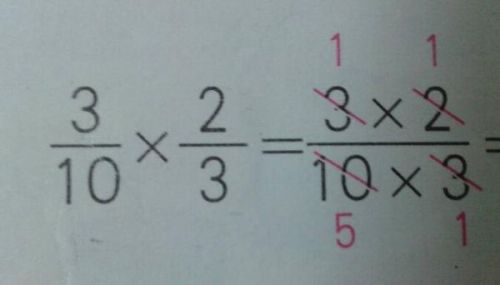
分子：部分的量化表达

分子，顾名思义，它代表的是分数所描述的具体部分或数量。在分数a/b中，a可以被理解为从某个整体中分割出来的特定数量或份数。例如，在分数1/4中，分子1表示从四个等份中取出的一个部分。因此，分子的大小直接决定了分数所表示的部分多少，是分数中“取多少”的直接体现。

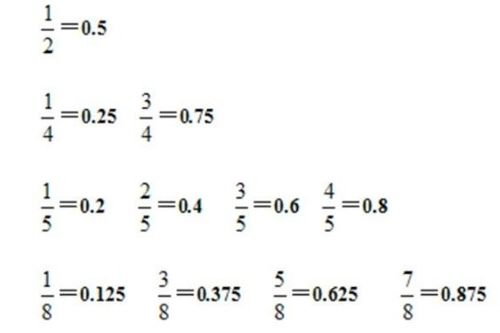
值得注意的是，分子可以是任何整数，包括正数、负数和零。正数分子表示取出的部分为正向量（如物品数量增加、时间延长等），负数分子则表示取出的部分为负向量（如物品数量减少、时间缩短等），而零分子则意味着没有取出任何部分，即分数值为零。

分母：整体的分割基准

与分子相对应，分母在分数中扮演着“整体”或“基准”的角色。它代表了将整体分割成多少等份，是分数比较和运算的基础。在分数a/b中，b即为分母，它告诉我们整体被均等地分成了b份。继续以1/4为例，分母4表明整体被分割成了四个等份，而分子1则代表我们取走了其中的一份。

分母同样可以是任何非零整数，其大小对分数值有着直接的影响。分母越大，意味着整体被分割得越细，每一份所占的比例就越小，因此分数值也随之减小；反之，分母越小，每一份所占的比例就越大，分数值则增大。

分子与分母的关系：比例与量化的桥梁

分子与分母之间通过分数线相连，共同构成了一个完整的分数，它们之间的关系是比例关系的直接体现。分数不仅表示了一个具体的数量（分子），还隐含了这个数量与整体（分母）之间的比例关系。这种比例关系使得分数在描述部分与整体、比率、比例等概念时具有无可比拟的优势。

在实际应用中，分数经常用于描述比例、百分比、比率等复杂概念。例如，在统计学中，我们常用分数来表示某一类别占总体的比例；在物理学中，分数则用于描述速度、加速度等物理量的变化率；在金融领域，分数则被广泛应用于计算收益率、利率等经济指标。

分数运算中的分子与分母

在分数的加减乘除运算中，分子与分母遵循着特定的规则。加法与减法要求先找到两个分数的最小公倍数作为通分母，然后将分子进行加减运算，结果作为新的分子；乘法则是直接将两个分数的分子相乘、分母相乘，得到新的分数；除法则是将除数分数取反（即变为倒数），然后与被除数分数相乘。这些运算规则确保了分数运算的准确性和一致性，同时也体现了分子与分母在分数运算中的不同作用和相互影响。

分子与分母的教学意义

在数学教育中，分子与分母的教学是分数教学的核心内容之一。通过引导学生理解分子与分母的含义及其相互关系，可以帮助学生建立起对分数概念的深刻理解，为后续学习比例、百分比、小数等数学内容打下坚实的基础。同时，分子与分母的教学也有助于培养学生的逻辑思维能力和抽象思维能力，使他们能够更好地理解和运用数学知识解决实际问题。

总结

综上所述，分子与分母作为分数的两个基本组成部分，它们各自承载着特定的数学意义和应用价值。分子代表了从整体中取出的部分数量或比例，而分母则定义了整体被分割的基准和单位。通过它们之间的相互作用和运算规则，分数能够精确地描述和比较不同数量之间的比例关系。因此，在学习和理解分数时，深入理解分子与分母的含义及其相互关系是至关重要的。这不仅有助于我们更好地掌握分数这一基础数学概念，还能为我们在数学、科学、经济等领域的学习和实践提供有力的支持。