平行四边形面积计算的绝妙方法

在几何学的奇妙世界里，隐藏着无数形状与面积的奥秘，而平行四边形，作为这个大家庭中的一员，不仅因其独特的对称美而引人注目，更因其面积计算的巧妙方法而让人着迷。想象一下，你站在一片由平行四边形铺就的草地上，微风拂过，草浪起伏，你是否好奇，这片绿意盎然的面积究竟有多大？今天，就让我们一同揭开平行四边形面积计算的神秘面纱，探索那些简单却强大的数学法则，让你的数学之旅更加丰富多彩。

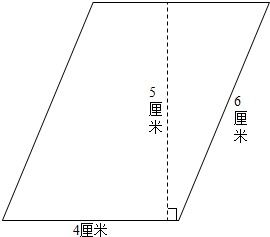
一、走进平行四边形的世界

平行四边形，一个拥有两组对边分别平行且等长的四边形，它在生活中无处不在：从一块规整的农田，到一扇滑动门的设计，再到一本打开的书籍，平行四边形以其特有的方式，融入了我们的日常。它不仅是几何图形的经典代表，更是解决实际问题中不可或缺的工具。了解它的面积计算方法，就如同掌握了一把打开几何大门的钥匙，让你在面对各种形状与尺寸的挑战时，更加游刃有余。

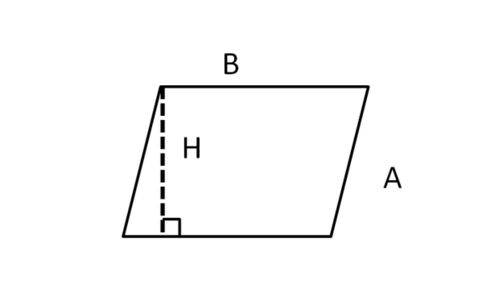
二、平行四边形面积的奥秘：从基础到深入

2.1 基础公式：底乘以高

谈及平行四边形的面积计算，最直接且广为人知的方法便是“底乘以高”。这里的“底”指的是平行四边形任意一边的长度，而“高”则是从这条边到它的对边（平行且不重合的边）的最短垂直距离。想象一下，如果你手里拿着一把尺子，垂直于平行四边形的一条边进行测量，那把尺子所量的长度，便是该平行四边形的高。通过简单的乘法运算，底与高的乘积便给出了平行四边形的面积。这个公式简单直观，易于操作，是解决大多数平行四边形面积问题的首选。

2.2 公式背后的逻辑：面积的分解与重组

那么，为什么“底乘以高”能够准确计算出平行四边形的面积呢？这背后隐藏着一个几何学的奥秘——面积的分解与重组。你可以尝试将一个平行四边形沿着其一条对角线切开，分成两个等面积的三角形。对于任意一个三角形，其面积计算公式也是“底乘以高的一半”。由于平行四边形的两个三角形共享同一条高，且底边之和等于平行四边形的边长，因此两个三角形的面积之和，正好是平行四边形面积的完整表达，即“底乘以高”。这一发现，不仅加深了我们对平行四边形面积公式的理解，也揭示了几何学中形状变换与面积守恒的深刻原理。

三、实践应用：让数学活起来

理论知识固然重要，但将其应用于实际生活中，才能真正感受到数学的魅力。想象一下，你是一名园艺师，需要为一块平行四边形形状的花园计算所需草坪种子的数量。这时，你只需要测量出花园的一条边长和相应的高，代入“底乘以高”的公式，就能轻松得出花园的面积，进而根据每平方米所需的种子量，计算出总需量。这样的实践，不仅让数学计算变得生动有趣，也极大地提高了我们解决问题的能力。

再来看一个例子，如果你是一名建筑师，设计了一扇平行四边形形状的滑动门，为了确保门板的稳固与安全，你需要准确计算出门的面积，以便选择合适的材料和重量。通过同样的“底乘以高”公式，你可以迅速得出答案，为接下来的设计步骤提供有力的数据支持。

四、拓展思维：探索更多可能

虽然“底乘以高”是计算平行四边形面积最直接的方法，但在某些特定情境下，我们也可以通过其他途径来求解。比如，如果你知道平行四边形的周长和一对相邻边的夹角，就可以利用三角函数来推算面积。此外，如果平行四边形嵌入在一个更大的矩形或三角形中，你还可以尝试通过整体面积减去其他已知形状的面积来间接求解。这些方法的灵活运用，不仅拓宽了我们的解题思路，也展示了数学解决问题的多样性和灵活性。

五、结语：让数学成为探索世界的钥匙

总而言之，平行四边形的面积计算，不仅仅是一个数学公式那么简单，它背后蕴含的是几何学的智慧与魅力。通过这一小小的知识点，我们不仅能够解决日常生活中的实际问题，更能在这个过程中，培养逻辑思维、空间想象以及解决问题的能力。让数学成为我们探索世界的钥匙，用它去解锁未知，发现美好。下次当你再次遇到平行四边形时，不妨停下脚步，用心去感受它的形状之美，用数学去揭开它的面积之谜，相信你会有更多意想不到的收获。

在这个充满奇迹的几何世界里，让我们继续前行，用数学的眼光观察世界，用知识的力量改变生活。平行四边形的面积计算，只是这段旅程中的一个小小起点，更多的精彩，正等待着我们一一揭晓。