如何判断一个图形是否为中心对称图形?
作者:佚名 来源:未知 时间:2024-10-31
怎样判断一个图形是否是中心对称图形
在平面几何中,中心对称图形是一种具有特殊性质的图形。一个图形如果绕某一点旋转180度后能够与自身重合,那么这个图形就被称为中心对称图形,该点则被称为对称中心。理解并判断一个图形是否是中心对称图形,可以通过以下几个步骤和方法进行。
首先,明确中心对称图形的定义和性质。一个图形是中心对称的,当且仅当图形中存在一个点,使得图形关于这个点旋转180度后,每个点都与其对称点重合。换句话说,在图形上任取一点P,都能够在图形上找到另一个点P',使得点P和点P'关于对称中心O对称,且线段OP和线段OP'长度相等、方向相反。
其次,观察图形的整体形状。如果图形在视觉上呈现某种“镜像”效果,即图形的一部分与另一部分在绕某一点旋转180度后可以完全重合,那么这个图形很可能是中心对称的。例如,正方形、圆形和正六边形等,都具有这种明显的中心对称特性。这些图形在旋转180度后,其形状和大小都不会发生改变,只是方向相反。
接下来,寻找图形的对称中心。对称中心是判断一个图形是否为中心对称的关键。通常,对于规则的多边形(如正方形、正三角形、正六边形等),其对称中心往往是多边形的几何中心;对于圆形,对称中心则是圆心。在寻找对称中心时,可以试着在图形上画一个点,然后绕这个点旋转图形180度,看看图形是否能够与自身重合。如果能够重合,那么这个点就是对称中心。
此外,利用图形的对称性质进行验证。如果图形是中心对称的,那么图形上的任意两点关于对称中心对称。具体来说,如果点A和点B是关于对称中心O对称的两点,那么线段OA和线段OB的长度应该相等,且方向相反。可以利用这一性质来验证图形是否为中心对称。例如,在正方形中,可以选择正方形的一个顶点作为点A,然后找到其关于正方形中心的对称点B(通常是正方形的另一个对角顶点)。通过测量线段OA和线段OB的长度,并比较它们的方向和大小,可以验证正方形是否是中心对称的。
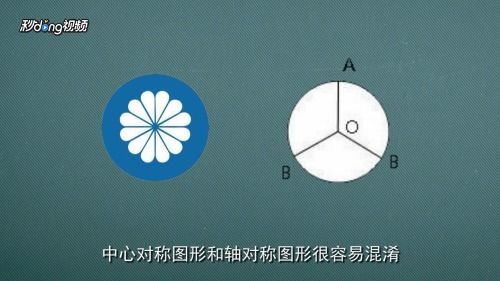
同时,注意区分中心对称和轴对称。虽然中心对称和轴对称都是图形的一种对称性质,但它们是有区别的。轴对称图形是关于某条直线(对称轴)对称的,而中心对称图形则是关于某个点(对称中心)对称的。在判断一个图形是否为中心对称时,要注意不要与轴对称混淆。例如,等腰三角形是轴对称图形,但不是中心对称图形,因为它不能绕某一点旋转180度后与自身重合。
在判断一些复杂图形时,可能需要结合多种方法。对于一些不规则的图形或者组合图形,可能无法直接通过观察或测量来判断其是否为中心对称。这时,可以尝试将图形分解成更简单的部分,然后分别判断这些部分是否为中心对称。如果每个部分都是中心对称的,并且它们的对称中心相同,那么整个图形也可能是中心对称的。另外,还可以利用计算机绘图软件或数学软件进行模拟和验证。这些软件通常具有旋转、平移和缩放等功能,可以帮助用户更直观地观察和判断图形的对称性质。
值得注意的是,一些特殊图形虽然具有某种对称性质,但并不是中心对称图形。例如,平行四边形中的矩形和菱形是轴对称图形,但不是所有平行四边形都是中心对称图形(只有当平行四边形的对角线互相平分且相等时,它才是中心对称图形)。同样地,等腰梯形是轴对称图形,但不是中心对称图形。在判断这些特殊图形时,需要特别注意它们的对称性质。
另外,通过实际生活中的例子来加深理解。许多自然界和人造物品中的图形都是中心对称的。例如,花朵的花瓣、雪花的形状、汽车的标志等。这些图形都具有明显的中心对称特性,可以通过观察它们来加深对中心对称图形的理解。同时,也可以尝试自己动手绘制一些中心对称图形,通过实践来巩固所学知识。
最后,总结判断一个图形是否是中心对称图形的方法:首先明确中心对称图形的定义和性质;然后观察图形的整体形状是否呈现“镜像”效果;接着寻找图形的对称中心并验证其是否正确;最后利用图形的对称性质进行进一步验证。如果以上步骤都符合中心对称图形的特征,那么就可以确定这个图形是中心对称的。
通过以上方法和步骤,我们可以准确地判断一个图形是否是中心对称图形。这种判断方法不仅适用于平面几何中的简单图形,也适用于更复杂的组合图形和三维图形。掌握这一技能有助于我们更好地理解几何图形的性质和应用。
- 上一篇: 阿尔及利亚是哪个国家的误解,真相揭晓!
- 下一篇: 如何正确书写信封的格式?






























