平行四边形和三角形,哪些是中心对称图形?
作者:佚名 来源:未知 时间:2024-10-31
在几何学的广阔领域中,中心对称图形是一个引人入胜的概念,它揭示了图形在特定操作下的独特性质。当我们提到“什么是中心对称图形”时,实际上是在探索那些关于点对称的图形,即图形关于某一点对称,该点称为对称中心。如果图形上的任意一点关于对称中心的对称点都在图形上,则这个图形就是中心对称图形。这个概念不仅在数学中占据重要地位,而且在日常生活和艺术设计中也频繁出现,为我们提供了丰富的视觉美感。
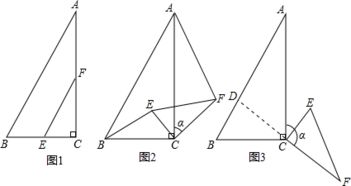
平行四边形是中心对称图形的一个典型例子。平行四边形有两组平行的对边,其定义允许它拥有多种形态,如矩形、菱形、正方形等,但无论哪种形态,它们都共享一个共同特性——中心对称性。以矩形为例,其对称中心是两条对角线的交点。如果我们围绕这个点将矩形旋转180度,你会发现旋转后的图形与原图重合,这就是中心对称性的直观体现。对于菱形和正方形,情况同样如此,只是由于它们的边长和角度的不同,它们看起来更为特殊。例如,正方形的所有边等长且所有角都是直角,这使得它在旋转180度后与原图重合的同时,还具有其他对称性,如轴对称性。

为了更深入地理解平行四边形的中心对称性,我们可以尝试构建一个简单的实验。取一张纸,画一个平行四边形,然后找到它的对称中心(两条对角线的交点)。接下来,用剪刀沿着这个中心点剪开图形,将两部分分开,然后将其中一部分旋转180度。你会发现,这两部分可以完美地拼合在一起,形成一个完整的平行四边形。这个过程直观地展示了中心对称性的原理。
与平行四边形相比,三角形的情况则更为复杂。三角形作为最基本的几何图形之一,根据其边长和角度的不同,可以分为多种类型,如等边三角形、等腰三角形、不等边三角形等。然而,并非所有三角形都是中心对称图形。实际上,只有等边三角形(也称正三角形)在特定条件下才具有中心对称性,而这种情况下的对称中心通常是三角形的重心、垂心和外心重合的点,也就是三角形的几何中心。但需要注意的是,即使在这种情况下,三角形的中心对称性也不同于平行四边形的那种直观的180度旋转对称性。等边三角形的中心对称性更多地体现在其可以通过绕对称中心旋转特定角度(如120度或240度)后与原图形重合,但这种旋转并不是180度的简单旋转。
对于等腰三角形和不等边三角形来说,它们则完全不具备中心对称性。等腰三角形有一条对称轴(即高),使得图形关于这条轴对称,但这不是中心对称。不等边三角形则连轴对称性都没有,它的形状完全不规则,无法找到任何对称点或对称轴来使图形通过某种操作后与原图重合。
中心对称图形的概念在数学、物理、计算机科学以及艺术设计中都有广泛的应用。在数学中,中心对称性是研究图形变换和性质的重要工具;在物理学中,许多自然现象和物理过程都遵循着对称性的原则;在计算机科学中,图形处理和图像处理技术也大量利用了对称性来提高效率和准确性;在艺术设计中,对称性则是设计师们常用的手法之一,它能够使作品看起来更加和谐、美观。
此外,中心对称图形还与我们的生活息息相关。从自然界中的花朵、树叶到人造物品如建筑、家具、艺术品等,都可以看到中心对称性的影子。这些对称的图形和图案不仅给我们带来了美的享受,还蕴含着深刻的数学原理和科学规律。
总的来说,中心对称图形是一个既简单又复杂的几何概念。它简单在于其定义明确、易于理解;复杂则在于其在实际应用中的多样性和广泛性。无论是平行四边形还是三角形,它们都是几何学中不可或缺的一部分,而中心对称性则是它们独特的魅力所在。通过深入研究和理解这些图形的性质和应用,我们可以更好地把握自然界的奥秘和人类创造的智慧。同时,也能够将这些知识运用到实际生活中去,为我们的生活和工作带来更多的便利和美好。
- 上一篇: QQ快捷登录,加速你的网络体验!
- 下一篇: 如何正确发出翘舌音?






























