自然数具体指的是哪些数字？

自然数是指用以计量事物的件数或表示事物次序的数，即用数码0，1，2，3，4……所表示的数。自然数由0开始，一个接一个，组成一个无穷的集体。自然数有有序性、无限性两大基本特点。自然数在日常生活中起了很大的作用，人们广泛使用自然数。自然数是人类历史上最早出现的数，自然数在计数和测量中有着广泛的应用，人们还常常用自然数来给事物标号或排序。如城市的电话号码、门牌号，公路、铁路上的里程碑等均属自然数。

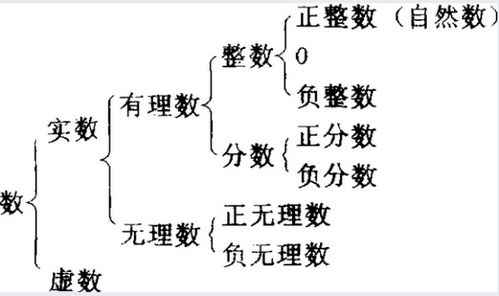
自然数的单位是“1”。自然数的集可以记作N={1,2,3,…}。自然数集N是一个可数的无穷集合。数学家一般以N*来表示不包括0的自然数集，而N表示包括0的自然数集。在数物体的时候，用来表示物体个数的数叫做自然数。一个物体也没有，用0表示，0也是自然数。0是最小的自然数，所有的自然数都是整数，最小的自然数是0，没有最大的自然数，自然数的个数是无限的。自然数通常用字母n表示，自然数的全体构成的集合叫做自然数集，自然数集常用符号N来表示。

在数学上，使用拉丁字母n来表示自然数，为了表示较大的数，还可以在n的前面加上小写或大写的拉丁字母来表示该数在字母表中的位置，这种方法称为数位的表示法。用数位表示法表示自然数时，把一个自然数写成数位形式，从高位到低位，一级一级地读，每一级末尾的0都不读出来，其他数位连续读几个0都只读一个零。例如，10005读作一万零五，而不是读成一万零零五。

自然数在日常生活中，有着极其广泛的应用，人们常常使用自然数来对事物进行计数，如物品的数量、人的年龄、身高、体重、长度、面积、体积、时间等。自然数还可以用来表示事物的顺序，如一周有七天，可用自然数1、2、3、4、5、6、7来表示；又如学生考试的名次，也可以用自然数来表示。

自然数的性质可以分为两大类：一类是基于其作为序数性质的，如：每个自然数都有一个后继者，n的后继者为n+1；每个自然数都小于其后继者，即n

自然数的加法、乘法运算可以在序数或基数理论中给出定义，并且两种定义下的运算是一致的。自然数的序数定义直接源于皮亚诺公理，其中规定了自然数的序数性质及其运算。自然数的基数定义则可以从集合论的角度入手。基于集合论的定义有多种方式，其中一种常见的定义方式是将自然数定义为有限集合的基数，即根据集合中元素的个数来定义自然数。这种定义方式的好处是直观且易于理解，但也存在一些问题，如需要事先定义有限集合和基数等概念。不过，在大多数数学分支中，这种定义方式是足够的，并且与皮亚诺公理给出的定义是一致的。

在自然数的运算中，加法与乘法是最基本的两种运算。在序数理论中，自然数的加法与乘法可以通过皮亚诺公理中的后继运算来定义。在基数理论中，则可以通过集合的并集与笛卡尔积来定义。两种定义方式下的加法与乘法运算均满足交换律、结合律以及分配律等基本性质。此外，自然数集中还可以定义序关系“<”，使得自然数集成为一个可排序的集合。序关系“<”可以通过后继运算或集合的包含关系来定义，两种定义方式下得到的序关系是一致的。

自然数集N是一个离散的、无穷的、可数的序数集合。它有以下几个基本特点：N中的元素是离散的，即它们之间存在空隙，不存在像实数那样的稠密性；N是无穷的，即它包含无穷多个元素，没有上界；N是可数的，即它的元素可以按某种规律一一列举出来。自然数集的这些特点使得它在数学中具有特殊的地位和作用。它是数学中许多重要概念的基础，如极限、级数、数列等都与自然数集密切相关。

自然数在人类历史的发展过程中起到了重要的作用。它不仅是数学中最基本的概念之一，也是物理学、化学、生物学等其他自然科学领域中不可或缺的基础概念。自然数的引入使得人们能够用数字来表示物体的数量、顺序以及大小关系等，从而极大地推动了人类社会的发展和进步。在现代社会中，自然数的应用更是无处不在。无论是计算机科学中的