f(x)与f'(x)之间的换算方法
作者:佚名 来源:未知 时间:2024-11-04
在数学领域中,函数f(x)与其导数f'(x)之间的关系是微积分学研究的核心内容之一。这两者之间不仅存在着定义上的直接联系,还在几何意义、物理应用、泰勒级数展开以及解决实际问题等多个维度上展现出深刻的换算关系。通过深入探索这些维度,我们能更加全面地理解f(x)与f'(x)之间的换算及其在数学、物理乃至工程学中的广泛应用。

一、定义与基础换算
首先,我们从定义上探讨f(x)与f'(x)的关系。函数f(x)表示自变量x与因变量y之间的一种对应关系,而f'(x)则是f(x)在x处的导数,描述了函数值随自变量变化的瞬时速率或斜率。在形式上,f'(x)通过极限运算定义为:
f'(x) = lim(Δx→0) [f(x+Δx) - f(x)] / Δx
这个定义表明,f'(x)是f(x)在x点切线斜率的数学表示。因此,从定义上看,f'(x)是f(x)的局部线性化近似,即在x附近的一个小区间内,f(x)的变化可以用一个线性函数(即切线)来近似。
二、几何意义的换算
几何上,f(x)与f'(x)之间的关系体现在切线与函数图像的关系上。对于函数y=f(x)的图像,如果在点P(x, f(x))处作一条切线,那么这条切线的斜率就是f'(x)。这个几何直观不仅帮助我们理解导数的概念,也为求解曲线的切线方程、法线方程等问题提供了便捷方法。
更进一步,f'(x)的正负决定了函数图像的增减性:当f'(x)>0时,函数在x附近是增函数;当f'(x)<0时,函数是减函数。而f'(x)=0的点,即临界点,则可能是函数的极大值点、极小值点或拐点,这些点的确定对于分析函数的整体形态至关重要。
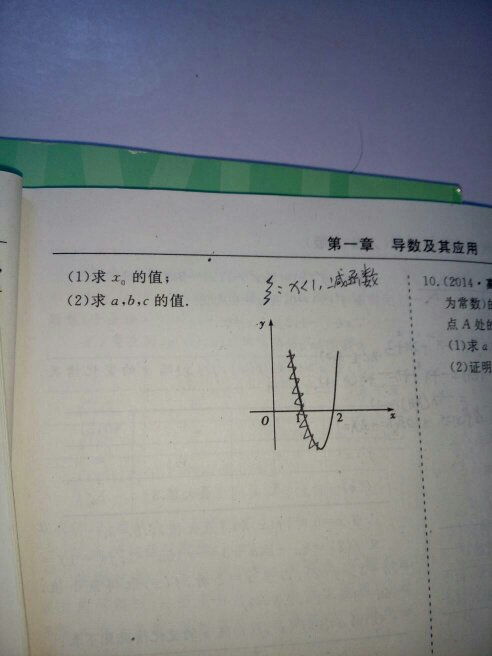
三、物理应用的换算
在物理学中,f(x)与f'(x)的换算关系体现在速度、加速度、位移等物理量的计算上。例如,在直线运动中,如果位移s是时间t的函数s=f(t),那么速度v就是位移函数s(t)的导数v=f'(t),加速度a则是速度函数v(t)的导数a=f''(t)(即s(t)的二阶导数)。
这种换算关系在力学、动力学等领域有着广泛的应用。例如,通过求解物体的运动方程,我们可以得到物体的速度、加速度等动力学参数,进而分析物体的运动状态和受力情况。
四、泰勒级数展开的换算
泰勒级数展开是微积分中的一个重要工具,它允许我们将一个复杂的函数表示为一个多项式级数。在这个级数中,每一项都涉及到f(x)在某点处的导数。具体来说,函数f(x)在x=a处的泰勒级数展开式为:
f(x) = f(a) + f'(a)(x-a) + f''(a)/2!(x-a)^2 + f'''(a)/3!(x-a)^3 + ...
这个级数展开不仅为我们提供了一种近似计算函数值的方法,还揭示了函数与其导数之间的内在联系。通过计算f(x)在不同点处的导数,我们可以逐步逼近f(x)的真实值,这对于解决一些难以直接求解的函数问题具有重要意义。
五、解决实际问题的换算
在实际问题中,f(x)与f'(x)的换算关系体现在优化问题、极值问题、稳定性分析等多个方面。例如,在经济学中,成本函数C=f(q)(q为产量)的导数C'(q)表示边际成本,即增加一单位产量所带来的成本变化。通过分析边际成本的变化规律,企业可以制定最优的生产计划。
在工程学领域,结构的稳定性和强度分析也常常涉及到f(x)与f'(x)的换算。例如,在梁的弯曲分析中,梁的挠度曲线y=f(x)的导数y'(x)表示梁的转角,而二阶导数y''(x)则与梁的弯矩和剪力密切相关。这些换算关系为结构的优化设计和安全性评估提供了重要依据。
六、结论
综上所述,f(x)与f'(x)之间的换算关系不仅体现在数学定义和几何直观上,还广泛应用于物理学、工程学以及经济学等多个领域。这种换算关系不仅加深了我们对函数性质的理解,也为解决实际问题提供了有力的数学工具。通过深入研究f(x)与f'(x)之间的内在联系,我们可以更加准确地把握事物的变化规律,为科学研究和工程实践提供有力的支持。
因此,在学习微积分的过程中,我们应该注重f(x)与f'(x)之间换算关系的理解和掌握,通过实际问题的应用
- 上一篇: 雪乡自由行攻略该怎么制定?
- 下一篇: 谷歌邮箱的后缀名,为何首选“@gmail.com”?
热门手游
换一换- 精品游戏
- 最热榜单




























