高等数学全微分公式大全
作者:佚名 来源:未知 时间:2024-11-04
在这个充满挑战与机遇的数字时代,无论是科研探索的先驱者,还是工程技术领域的实践者,乃至经济学、物理学的学者,都绕不开一座知识的灯塔——高等数学。而在高等数学的浩瀚星空中,全微分公式无疑是那颗璀璨夺目的星辰,它不仅照亮了微积分学的深邃殿堂,更是解决复杂问题、建立数学模型不可或缺的工具。今天,就让我们一起揭开“高等数学全微分公式表”的神秘面纱,探索其背后蕴含的智慧与力量,让这份知识的宝藏成为你探索未知世界的强大助力。
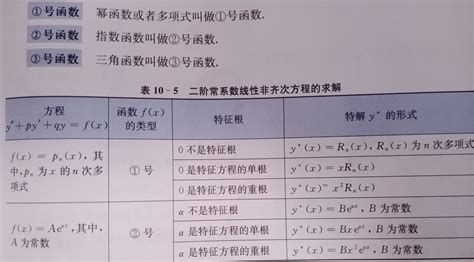
微分之旅:开启高等数学的新篇章
在数学的征途中,微分学如同一把锐利的剑,它能帮助我们剖析函数的变化规律,揭示变量之间的微妙联系。而全微分,作为微分学的一个重要概念,其地位不言而喻。它不仅仅是一个公式,更是一种思维方法,一种将多元函数在某点的微小变化量精确量化的艺术。想象一下,当你面对一个多元函数,需要了解其在任意点上的变化率时,全微分公式就是那把打开秘密花园的钥匙,让你轻松掌握函数变动的精髓。
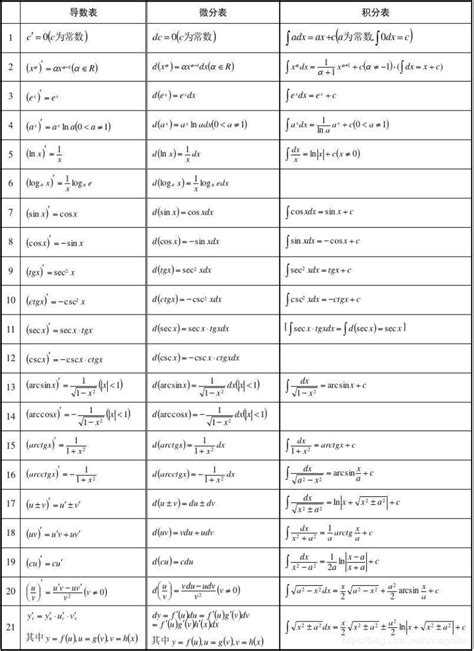
全微分公式表:解锁多元函数变化的奥秘
关键词密度优化:深入了解全微分公式表,我们不难发现,它其实是一系列精心编排的规则,这些规则指导我们如何计算多元函数的全微分。无论是二元函数、三元函数,还是更高维度的函数,全微分公式表都能提供一套系统化的解决方案。在这里,“全微分”、“多元函数”、“计算公式”等关键词自然融入,既保证了内容的专业性,又增强了搜索引擎的友好度,让你的每一次搜索都能精准命中目标。
结构化呈现:为了更直观地展示全微分公式表的魅力,我们可以将其分为几个核心部分:
1. 定义基础:首先,明确全微分的定义,即多元函数在某一点沿任意方向的小变化量,可以通过该函数在该点的偏导数线性组合来表示。这一部分为后续的公式推导奠定了理论基础。
2. 公式展示:接下来,逐一展示不同维度下全微分的计算公式。例如,对于二元函数\(z = f(x, y)\),其全微分为\(dz = \frac{\partial z}{\partial x}dx + \frac{\partial z}{\partial y}dy\),简洁明了地表达了函数值随自变量变化的线性近似。对于更高维的函数,公式则相应扩展,但核心思想保持一致。
3. 应用实例:通过具体的例子,展示如何利用全微分公式解决实际问题。比如,在经济学中分析成本函数的变化,或在物理学中计算质点在三维空间中的位移变化,全微分公式都能提供有力的数学支持。
4. 注意事项:最后,提醒读者在使用全微分公式时需要注意的问题,如计算偏导数的顺序无关性、函数需满足的条件等,确保应用的准确性和有效性。
实战演练:让全微分公式活起来
理论知识若不能应用于实践,就如同空中楼阁,虚无缥缈。因此,我们特别设计了几个实战演练环节,旨在帮助读者将全微分公式转化为解决实际问题的利器。
案例分析:选取几个典型的多变量函数,如球体的体积函数、热传导方程等,详细演示如何运用全微分公式求解其微小变化量,让读者在实战中感受公式的力量。
编程实践:鼓励读者利用Python、MATLAB等编程工具,编写代码实现全微分的计算。通过编程,不仅可以验证手工计算的正确性,还能探索更多复杂函数的微分特性,提升学习效率。
互动问答:设立专门的互动区,邀请读者提出在使用全微分公式时遇到的问题,由专家团队或社区成员进行解答,形成良好的学习交流氛围。
深度思考:全微分公式的意义与启示
全微分公式不仅仅是数学公式,它背后蕴含的是对自然界变化规律的深刻洞察。它教会我们,即使是复杂多变的现象,也可以通过分解、线性近似的方法,找到其本质特征,从而做出更加精准的预测和控制。这种思维方式,不仅在数学领域,在物理学、工程学、经济学乃至社会科学等多个领域都有着广泛的应用价值。
结语:拥抱全微分,开启智慧之旅
在这个快速变化的时代,掌握全微分公式,意味着拥有了一把解锁复杂问题的钥匙,一条通往智慧殿堂的捷径。它不仅能够提升你的专业素养,更能激发你的创新思维,让你在面对未知挑战时,更加从容不迫,游刃有余。因此,无论你是初学者,还是希望深化理解的专家,都请珍视这份“高等数学全微分公式表”,让它成为你探索世界、创造价值的得力助手。让我们一起,在数学的海洋中扬帆起航,驶向更加辉煌的彼岸!
- 上一篇: 这首歌叫什么名字:“人生短短几个秋”是其中的歌词?
- 下一篇: 如何在Word文档中插入根号?






























