如何计算一立方米体积

在数学、物理以及工程学等多个领域中，“一立方”的概念是普遍存在的，它指的是一个边长为1单位（例如1米、1厘米等）的正方体的体积。这一概念虽看似简单，但在不同学科和实际应用中却展现出丰富的内涵和多维度的理解。本文将从几何学、物理学、工程学以及实际应用等多个角度，探讨“一立方”的计算和应用。

几何学中的一立方

几何学是研究点、线、面、体及其性质的数学分支。在三维空间中，体是由平面围成的空间图形，而正方体则是最简单且对称的三维几何体之一。正方体有六个面，每个面都是一个正方形，十二条棱的长度相等。当正方体的每一条棱长为1单位时，其体积就是“一立方”。

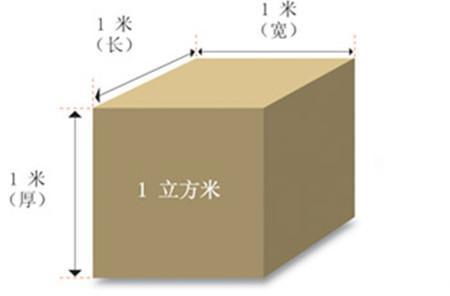
在几何学中，计算正方体的体积是基础中的基础。正方体的体积公式为V=a³，其中a为棱长。当a=1时，V=1³=1，即一立方。这个公式虽然简单，但它是几何学中许多复杂体积计算的基础，如长方体的体积、三棱柱的体积等，都可以通过分解或变形转化为正方体的体积进行计算。

物理学中的一立方

物理学是研究物质基本结构和运动规律的学科。在物理学中，“一立方”不仅是一个几何概念，还常常用来表示单位体积内的物理量，如密度、压强、电容率等。

密度是物理学中一个重要的物理量，它表示单位体积内物质的质量。其公式为ρ=m/V，其中m为质量，V为体积。当V=1立方时，ρ就表示单位体积内物质的质量，即密度。在气体、液体和固体的研究中，密度是一个关键的参数，它决定了物质的许多物理和化学性质。

压强是表示单位面积上受到的压力的物理量。虽然压强本身并不直接涉及体积，但在流体力学中，单位体积内的流体所产生的压强是一个重要的研究内容。此外，在气体状态方程中，如理想气体状态方程PV=nRT，体积V也是一个重要的变量。当体积为1立方时，可以研究在固定体积下压强、温度和物质的量之间的关系。

工程学中的一立方

工程学是将自然科学和数学原理应用于解决实际问题的学科。在工程学中，“一立方”常常用来表示工程材料的体积、结构物的尺寸等。

在建筑工程中，混凝土的用量常常以立方米为单位进行计算。在设计建筑结构时，需要根据建筑物的承载能力和稳定性要求，计算出所需混凝土的体积。一立方的混凝土通常作为设计和施工中的一个基准单位，用来评估工程的规模和成本。

在水利工程中，水库的容量、河流的流量等也常常以立方米为单位进行计量。这些参数的准确计算对于工程的安全运行和有效利用水资源至关重要。例如，在设计水库时，需要准确计算出水库的总容量和各个水位下的蓄水量，以确保水库在防洪、灌溉和发电等方面的功能得到有效发挥。

实际应用中的一立方

除了几何学、物理学和工程学之外，“一立方”还在许多实际应用中发挥着重要作用。这些应用涉及日常生活中的方方面面，如包装、物流、农业等。

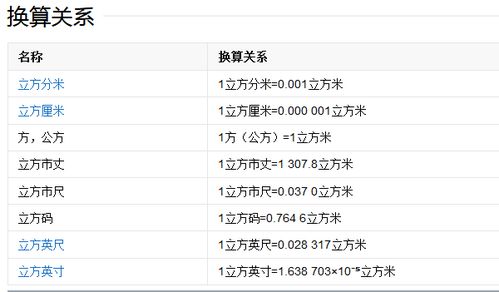
在包装行业中，货物的体积是评估运输成本和存储空间的重要指标。许多货物的包装尺寸都是按照立方厘米或立方米来设计的，以确保在运输和存储过程中能够充分利用空间并降低成本。一立方的概念在这里成为了评估包装效率和优化物流流程的重要依据。

在农业领域，土壤的体积和质量对于农作物的生长和产量有着重要影响。通过对土壤进行取样和分析，可以测量出单位体积内土壤的重量、含水量、养分含量等参数。这些参数对于指导农业生产、优化施肥方案和提高农作物产量具有重要意义。

此外，在环保和垃圾处理领域，“一立方”的概念也被广泛应用。通过对垃圾进行分类和压缩处理，可以大大减少垃圾的体积和重量，从而降低运输和处理成本。一立方的垃圾在压缩前后的体积变化成为评估垃圾处理效率和优化处理流程的重要指标。

总结

综上所述，“一立方”是一个具有广泛应用和多维度理解的概念。在几何学中，它是计算正方体体积的基础；在物理学中，它表示单位体积内的物理量；在工程学中，它用来表示工程材料的体积和结构物的尺寸；在实际应用中，它涉及包装、物流、农业等多个领域。通过深入了解“一立方”在不同领域中的应用和计算方法，我们可以更好地理解和利用这一概念，为解决实际问题提供有力的数学和物理支持。同时，我们也应该注意到，“一立方”作为一个简单的几何概念，在实际应用中却展现出丰富的内涵和广泛的应用前景，这也正是数学和物理学等基础学科在科学研究和工程实践中的重要价值所在。