完全平方公式十二大变形口诀详解
作者:佚名 来源:未知 时间:2024-11-04
完全平方公式是数学中的一个基础而重要的公式,它能帮助我们快速计算形如(a+b)²或(a-b)²的表达式。对于想要深入了解并掌握完全平方公式的朋友来说,了解它的12种变形口诀无疑会是一个巨大的助力。以下是这些口诀的详细解释:
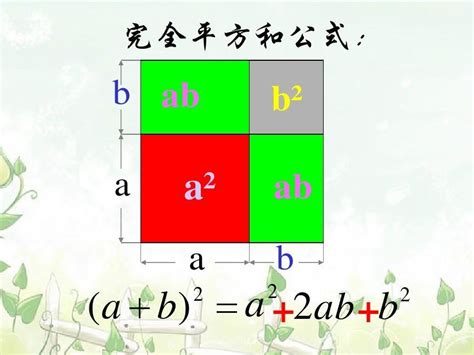
首先,最基本的完全平方公式是:

(a+b)²=a²+2ab+b²
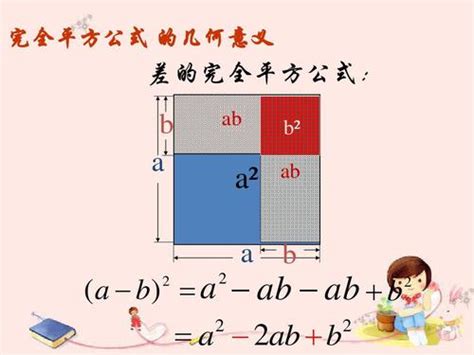
(a-b)²=a²-2ab+b²

这两个公式告诉我们,一个二项式的平方等于首项的平方加上或减去(取决于二项式中的符号)两倍的首尾项之积,再加上尾项的平方。这个规律可以通过以下的12种变形口诀来加深理解和记忆:
变形口诀一:
两平方项在两端,底积2倍在中部。
这个口诀强调了完全平方公式的结构:两个平方项(a²和b²)位于表达式的两端,而两个底数(a和b)的积的2倍位于中间。
变形口诀二:
同正两底和平方,全负和方相反数。
如果两个底数都是正数,那么他们的和的平方就是各自平方的和加上两倍的两底之积。如果两个底数都是负数,那么他们的平方和仍然是各自平方的和(因为负负得正),但在使用公式时需要注意符号的变化。
变形口诀三:
分成两底差平方,方正倍积要为负。
当计算两个底数之差的平方时,公式中的倍积项(2ab)的符号会变为负。
变形口诀四:
两边为负中间正,底差平方相反数。
如果在完全平方公式中,我们把a和b都看作负数(或者说,我们考虑-a和-b的平方),那么在计算差平方时,结果会是正的(因为负负得正),但需要注意的是,这时候的倍积项仍然是负的,所以在形式上看起来就像是“底差平方的相反数”,但实际上是因为我们改变了底数的符号。
变形口诀五:
一平方又一平方,底积2倍在中路。
这个口诀再次强调了完全平方公式的结构,即两个平方项和两倍底积的组合。
变形口诀六:
三正两底和平方,全负和方相反数。
这里的“三正”可能是一个口误或笔误,更可能的理解是强调在完全平方公式中,如果底数(或底数的相反数)的符号一致,则他们的平方和(或差)可以按照完全平方公式来计算。如果都是负数,那么在计算时需要注意符号的变化。
变形口诀七:
分成两底差平方,两端为正倍积负。
这个口诀再次强调了差平方的公式,即(a-b)²=a²-2ab+b²,其中倍积项的符号为负。
变形口诀八:
两边若负中间正,底差平方相反数(与前述口诀四类似,但强调了两边为负的情况)。
这个口诀是对变形口诀四的进一步阐释,强调了当底数为负数时,差平方的符号变化。
变形口诀九(公式变形应用):
a²+b²=(a+b)²-2ab
这个公式变形告诉我们,可以通过计算(a+b)²然后减去两倍的两底之积来得到a²和b²的和。
变形口诀十(公式变形应用):
a²+b²=(a-b)²+2ab
同样地,我们也可以通过计算(a-b)²然后加上两倍的两底之积来得到a²和b²的和。
变形口诀十一(公式变形应用):
(a+b)²-(a-b)²=4ab
这个公式变形揭示了(a+b)²和(a-b)²之间的关系,即他们的差等于四倍的两底之积。
变形口诀十二(公式变形应用及完全平方式):
a²+b²+c²=(a+b+c)²-2(ab+ac+bc)
这个公式变形将完全平方公式的应用范围扩展到了三个数的情况,它告诉我们三个数的平方和等于这三个数的和的平方减去他们两两之间的积的两倍。
此外,还有一些与完全平方公式相关的公式和性质,如:
(a+b+c)²=a²+b²+c²+2ab+2ac+2bc
这个公式告诉我们三个数的和的平方等于他们各自的平方和加上他们两两之间的积的两倍。
以及,如果一个数能够表示为另一个数的平方,那么这个数就被称为平方数。而一个代数式如果能够被还原为(ab)²的形式






























