快速计算1到100之和的简便方法
作者:佚名 来源:未知 时间:2024-11-14
在我们日常的学习和生活中,经常会遇到需要计算一系列数字之和的情况,比如从1加到100。这种计算看似简单,但如果直接逐个相加,不仅耗时耗力,还容易出错。幸运的是,数学为我们提供了一种简便的方法来计算从1加到100的和,即利用高斯求和公式。下面,我们就来详细探讨一下这个简便方法,以及它是如何被发现和应用的。
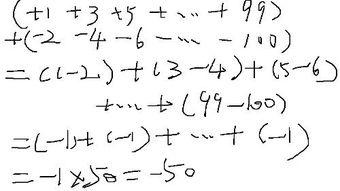
高斯求和公式的核心思想是将从1到100的这些数字进行配对,使得每一对的和都是一个相同的数。具体来说,我们可以将1和100、2和99、3和98等依次配对,直到50和51。这样,每一对的和都是101。由于一共有50对这样的数字,所以我们可以直接将101乘以50来得到最终的和。这种方法不仅大大简化了计算过程,还提高了计算的准确性。
关于高斯求和公式的由来,有一个广为流传的故事。高斯是德国的一位杰出数学家,他在很小的时候就展现出了非凡的数学天赋。据说,在高斯上小学的时候,他的数学老师出了一道题,要求学生们计算从1加到100的和。其他同学都在忙着逐个相加,而高斯却很快就给出了答案。当老师问他是如何这么快就得出答案时,高斯解释了他的配对方法。老师对此感到非常惊讶和欣喜,他意识到高斯有着非凡的数学才能。
这个故事不仅展示了高斯在数学方面的天赋,也揭示了高斯求和公式的独特之处。这个公式不仅适用于从1加到100的情况,还可以推广到其他类似的求和问题中。只要我们能够将需要求和的数字进行恰当的配对,使得每一对的和都是一个相同的数,就可以利用这个公式来简化计算。
那么,为什么高斯求和公式会如此有效呢?这主要得益于数学中的对称性和等差数列的性质。从1到100的这些数字构成了一个等差数列,其中每一项与前一项的差都是一个常数(在这里是1)。而高斯求和公式正是利用了这种等差数列的对称性来简化计算的。通过将数字进行配对,我们使得每一对的和都相等,从而可以将求和问题转化为乘法问题,大大降低了计算的复杂度。
除了高斯求和公式之外,还有其他一些方法可以用来计算从1加到100的和。比如,我们可以利用数学中的级数求和公式或者编写一个程序来进行计算。然而,这些方法要么比较复杂难以理解,要么需要借助计算机等工具来实现。相比之下,高斯求和公式更加直观易懂、易于操作,因此在实际应用中更加受欢迎。
当然,高斯求和公式的应用并不仅限于计算从1加到100的和。它还可以被用来解决其他类似的求和问题,比如计算从1加到任意正整数n的和,或者计算某个等差数列的和等。在这些情况下,我们只需要将高斯求和公式中的100替换为相应的n值或者等差数列的末项值,就可以轻松地得到答案。
此外,高斯求和公式还可以被推广到更复杂的数学问题中。比如,在计算某些特定类型的级数和时,我们可以利用高斯求和公式的思想来找到简化计算的方法。这些应用不仅展示了高斯求和公式的广泛适用性,也进一步证明了数学在解决实际问题中的重要作用。
总的来说,从1加到100的简便方法——高斯求和公式是一种非常实用且高效的计算方法。它利用了数学中的对称性和等差数列的性质来简化计算过程,使得我们能够在短时间内得到准确的结果。无论是在学习、工作还是生活中,掌握这个简便方法都将对我们大有裨益。
在实际应用中,我们可以将高斯求和公式应用于各种需要求和的场合中。比如,在统计学中计算数据的总和时,我们可以利用这个公式来快速得到结果;在物理学中计算物体的总质量或者总能量时,我们也可以借助这个公式来简化计算过程。此外,在编程中处理大规模数据时,我们也可以利用高斯求和公式的思想来优化算法、提高计算效率。
当然,在学习和使用高斯求和公式的过程中,我们也要注意避免一些常见的错误。比如,有些人可能会误解公式中的n值含义,将其错误地解释为需要求和的数字个数而不是末项值;还有些人可能会在计算过程中忽略掉配对后剩余的单个数字(如果有的话),从而导致结果不准确。因此,在使用高斯求和公式时,我们需要仔细审题、明确公式中各符号的含义,并严格按照步骤进行计算。
总之,从1加到100的简便方法——高斯求和公式是一种非常实用的计算方法。它利用了数学中的对称性和等差数列的性质来简化计算过程,使得我们能够在短时间内得到准确的结果。无论是在学习、工作还是生活中,掌握这个简便方法都将对我们产生积极的影响。希望这篇文章能够帮助大家更好地理解高斯求和公式及其在实际应用中的价值。
- 上一篇: 怎么做爆炒腰花?
- 下一篇: 揭秘迪拜:这座璀璨之城究竟归属于哪个国家?






























