掌握三角函数公式，轻松解决数学难题！

在数学的浩瀚宇宙中，三角函数如同一颗璀璨的星辰，以其独特的魅力和广泛的应用，照亮了无数学子的求知之路。它不仅是解决几何问题的利器，更是物理、工程乃至天文学等领域不可或缺的工具。今天，就让我们一同揭开三角函数公式的神秘面纱，探索它们背后的奥秘，看看这些公式是如何成为连接现实与理论的桥梁。

初识三角函数：角度与边的舞蹈

想象一下，你站在一个巨大的圆形舞台上，圆心就是你的立足点，半径则是你伸展出去的手臂。当你绕着圆心旋转，手臂与某条固定直线（比如舞台的边缘线）之间的夹角不断变化，这时，你的手臂长度（半径）不变，但手臂末端到达舞台边缘的点的位置却在不断变化。这个场景，正是三角函数诞生的舞台。

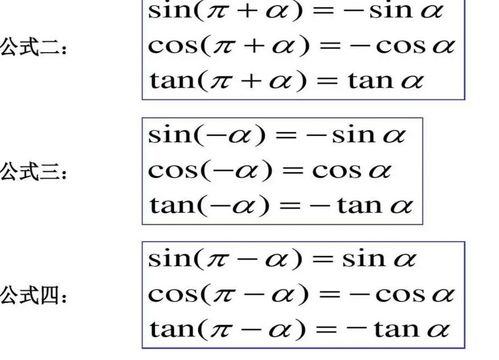
三角函数，顾名思义，是涉及三角形的一类函数，主要包括正弦（sin）、余弦（cos）、正切（tan）、余切（cot）、正割（sec）和余割（csc）六种。其中，正弦、余弦和正切是最为基础且常用的三种。它们通过直角三角形边长与角度的关系来定义，是连接几何与代数的桥梁。

正弦（sin）：在任意直角三角形中，对边与斜边的比值。记作sinθ，其中θ为锐角。

余弦（cos）：在任意直角三角形中，邻边与斜边的比值。记作cosθ。

正切（tan）：在任意直角三角形中，对边与邻边的比值。记作tanθ。

三角函数公式的奇幻之旅

基础公式：定义出发

从定义出发，我们得到了三角函数最基本的表达式。但真正让三角函数变得强大的，是它们在不同情境下的转换公式、和差公式、倍角公式以及半角公式等。这些公式如同魔法师的咒语，能够将复杂的计算简化，让问题的求解变得轻松。

和差公式：角度的加减法

想象一下，你站在舞台上，先旋转了一个角度θ，再旋转另一个角度φ，那么你总共旋转了多少度呢？自然是θ+φ或θ-φ。三角函数的和差公式正是解决这类问题的钥匙。

正弦和差公式：sin(θ+φ) = sinθcosφ + cosθsinφ

sin(θ-φ) = sinθcosφ - cosθsinφ

余弦和差公式：cos(θ+φ) = cosθcosφ - sinθsinφ

cos(θ-φ) = cosθcosφ + sinθsinφ

正切和差公式：tan(θ+φ) = (tanθ + tanφ) / (1 - tanθtanφ)

tan(θ-φ) = (tanθ - tanφ) / (1 + tanθtanφ)

倍角公式：角度的倍增

如果说和差公式是角度的加减法，那么倍角公式就是角度的乘法。它告诉我们，当一个角度翻倍时，对应的三角函数值会如何变化。

正弦倍角公式：sin2θ = 2sinθcosθ

余弦倍角公式：cos2θ = cos²θ - sin²θ 或 cos2θ = 1 - 2sin²θ 或 cos2θ = 2cos²θ - 1

正切倍角公式：tan2θ = (2tanθ) / (1 - tan²θ)

半角公式：角度的减半

与倍角公式相对应，半角公式则揭示了角度减半时，三角函数值的变化规律。

正弦半角公式：sin(θ/2) = ±√[(1 - cosθ) / 2]

余弦半角公式：cos(θ/2) = ±√[(1 + cosθ) / 2]

正切半角公式：tan(θ/2) = ±√[(1 - cosθ) / (1 + cosθ)] = (1 - cosθ) / sinθ = sinθ / (1 + cosθ)

辅助角公式：隐藏的角色

在某些复杂表达式中，通过引入一个辅助角，可以大大简化计算。辅助角公式就像是数学中的变形术，让复杂的表达式变得简洁明了。

辅助角公式：a·sinθ + b·cosθ = √(a² + b²)·sin(θ + φ)，其中tanφ = b/a

万能公式：一“式”解千愁

万能公式是三角函数公式中的佼佼者，它仅用tan(θ/2)就能表示出sinθ、cosθ和tanθ的所有形式，几乎可以替代所有其他三角函数公式。

正弦万能公式：sinθ