扇形周长计算公式
作者:佚名 来源:未知 时间:2024-11-06
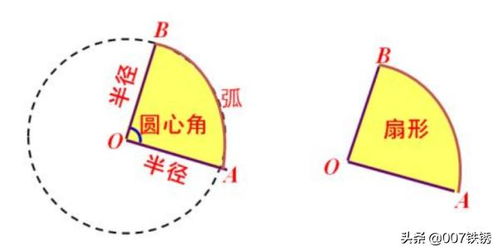
扇形,作为几何学中常见的平面图形之一,其独特的形状和性质在日常生活和科学研究中有着广泛的应用。当我们想要计算扇形的周长时,首先需要明确扇形的定义及其构成元素。扇形是由一个圆心和两条半径以及圆心角所围成的部分圆,其周长不仅包含这两条半径,还包含一条与圆心角相对应的弧。因此,扇形的周长计算相对圆而言稍显复杂,但掌握了正确的公式和步骤后,便能轻松求解。
扇形的周长求解公式
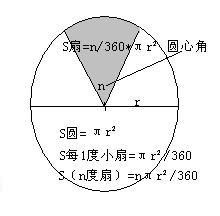
扇形周长的计算公式为:C = 2r + l,其中C代表扇形的周长,r为扇形的半径,l为扇形的弧长。这个公式直观地反映了扇形周长的构成:两条半径的长度加上一条弧的长度。
半径r的确定
在计算扇形周长之前,首先需要确定扇形的半径r。半径是从圆心到扇形边缘的线段长度,它决定了扇形的大小和形状。在实际应用中,半径r通常通过测量或已知条件给出。
圆心角与弧长的关系
扇形周长中的另一个关键元素是弧长l。弧长与扇形的圆心角θ密切相关。圆心角θ是扇形所对应的圆的部分角度,通常以度数或弧度为单位表示。在圆的周长公式C = 2πr中,整个圆的周长与半径r和圆周率π有关。对于扇形而言,其弧长l则是整个圆周长的一部分,具体比例由圆心角θ决定。

在弧度制下,弧长l与圆心角θ和半径r的关系可以表示为:l = θ × r。这里需要注意的是,θ应以弧度为单位。若θ以度数为单位,则需要先将其转换为弧度。度数与弧度的转换公式为:弧度 = 度数 × (π/180)。
扇形周长计算步骤
1. 确定半径r:根据题目条件或测量结果确定扇形的半径。
2. 确定圆心角θ:根据题目条件确定扇形的圆心角,注意其单位(度数或弧度)。若以度数为单位,需进行单位转换。
3. 计算弧长l:根据弧长公式l = θ × r(θ为弧度)或l = 度数 × (π/180) × r(θ为度数)计算扇形的弧长。
4. 计算周长C:将半径r和弧长l代入扇形周长公式C = 2r + l,得到扇形的周长。
实例分析
为了更好地理解扇形周长的计算过程,我们可以通过一个实例进行分析。
实例:一个扇形的半径为5cm,圆心角为90°(即π/2弧度)。求该扇形的周长。
解题步骤:
1. 确定半径r:r = 5cm。
2. 确定圆心角θ:θ = 90°,需转换为弧度制。θ(弧度) = 90° × (π/180) = π/2。
3. 计算弧长l:l = θ × r = (π/2) × 5 = 5π/2 cm(注意,这里π为圆周率,取近似值3.14时,l ≈ 7.85cm)。
4. 计算周长C:C = 2r + l = 2 × 5 + 5π/2 = 10 + 5π/2 cm(同样地,取π的近似值时,C ≈ 17.85cm)。
通过上述步骤,我们得出了该扇形的周长约为17.85cm。
扇形周长的应用场景
扇形周长的计算在多个领域都有着广泛的应用。例如,在建筑设计中,扇形窗户或门的周长计算有助于确定所需的材料数量和成本;在机械工程中,扇形齿轮或扇形叶片的周长计算对于设计和制造过程至关重要;在物理学和天文学中,扇形区域的光照强度或辐射强度计算往往也涉及到扇形周长的概念。
注意事项
1. 单位统一:在计算扇形周长时,应确保所有相关量(如半径、圆心角)的单位统一。特别是圆心角,在弧度制和度数制之间进行转换时要特别注意。
2. 精确计算:虽然在实际应用中,我们通常会取圆周率π的近似值进行计算,但在需要高精度结果的场合,应使用更精确的π值。
3. 理解公式:掌握扇形周长公式的推导过程和构成元素,有助于更深入地理解扇形的几何性质。
结语
扇形作为几何学中的重要图形,其周长的计算不仅涉及基本的数学运算,还涉及到对扇形几何性质的理解和应用。通过本文的介绍,我们了解了扇形周长的
- 上一篇: 解锁雪的笔顺,轻松掌握书写秘诀!
- 下一篇: 家常炒酸奶的简单制作方法






























