常微分方程的通解公式是怎样的?
作者:佚名 来源:未知 时间:2024-11-06
在数学的浩瀚领域中,常微分方程(Elementary differential equations)是连接理论与实践的重要桥梁。它们广泛应用于物理、工程、经济学等多个领域,帮助人们理解和预测各种自然现象和人工系统的行为。今天,我们就来详细探讨一下常微分方程通解公式的各个方面,让这一数学概念变得通俗易懂。
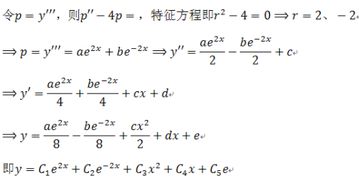
常微分方程的基本概念
首先,让我们明确一下什么是微分方程。微分方程是含有未知函数的导数或微分的方程。当这些方程中只涉及一个自变量(如时间t或空间坐标x)和一个因变量(通常是某种物理量,如速度v或位移s)及其导数时,我们称之为常微分方程。与之相对的,涉及多个自变量和因变量及其偏导数的方程则称为偏微分方程。

常微分方程可以按照其最高阶导数的阶数进行分类,如一阶常微分方程、二阶常微分方程等。而求解这些方程,我们的目标是找到未知函数y(通常表示为x的函数)的表达式。
通解与特解
在求解常微分方程时,我们经常会遇到两个重要的概念:通解和特解。
通解:是微分方程的一个解,它包含了所有可能的解(或解的一部分),通常表现为一个或多个任意常数的形式。这些常数的数量恰好等于方程的阶数。例如,对于一阶微分方程,通解将包含一个任意常数C;对于二阶微分方程,则包含两个任意常数C1和C2,以此类推。
特解:是微分方程的一个具体解,它不包含任意常数。特解通常通过给定初始条件(如y(x0)=y0)来确定。换句话说,特解是通解在满足特定条件下的一个实例。
值得注意的是,通解不一定包含所有的特解。有些特解可能因不满足通解中的某些条件而被排除在外,这些特解被称为奇解。
常微分方程通解公式的形式
在初等数学中,我们接触到了各种形式的方程,如线性方程、二次方程等。常微分方程的通解公式也有其特定的形式,通常表示为y=φ(x),其中φ(x)是一个函数,它可能是x的显式函数(如y=sin(x+C)),也可能是隐式函数(如φ(x,y)=0)。
对于一阶常微分方程,其通解公式的形式可能因方程类型的不同而有所差异。例如:
可分离变量的方程:形如f1(x)dx=f2(y)dy的方程,可以通过对两边分别积分来求解,得到通解∫f1(x)dx=∫f2(y)dy+C。
一阶线性微分方程:形如dy/dx+P(x)y=Q(x)的方程,其通解可以通过常数变易法求得,形式为y=e-∫P(x)dx[∫e∫P(x)dx·Q(x)dx+C]。
对于更高阶的常微分方程,求解过程可能更加复杂,但基本思路仍然是找到包含任意常数的解,这些常数通过方程的阶数来确定。
求解常微分方程的方法
求解常微分方程的方法多种多样,以下是一些常见的方法:
1. 分离变量法:这是求解一阶常微分方程最基本的方法之一。当方程可以写为f1(x)dx=f2(y)dy的形式时,可以通过对两边分别积分来求解。
2. 常数变易法:这种方法主要用于求解一阶线性微分方程。它基于一个观察:对于形如dy/dx+P(x)y=Q(x)的方程,如果Q(x)=0,则方程变为dy/dx+P(x)y=0,这是一个齐次方程,其解可以通过分离变量法求得。对于非齐次方程,我们可以假设其解具有齐次方程解的形式,但其中的常数需要替换为一个关于x的函数,然后通过求解得到的新的微分方程来确定这个函数。
3. 积分因子法:这种方法用于求解一阶非齐次线性微分方程,特别是当方程不能通过常数变易法直接求解时。积分因子的作用是使原方程变为一个恰当方程(即其左侧可以表示为某个函数的全微分),从而可以通过积分求解。
4. 降阶法:对于二阶或更高阶的常微分方程,有时可以通过适当的变量替换或变换将其降为一阶方程来求解。例如,对于二阶缺y型方程y''=f(x,y'),可以令y'=p,则y''=dp/dx,从而将原方程转化为一阶方程dp/dx=f(x,p)。
5. 幂级数解法:这种方法适用于求解某些类型的非线性微分方程。它基于一个假设:方程的解可以表示为x的幂级数的形式,然后通过将级数代入方程并比较各项
- 上一篇: 行人与人行横道及徒步标志的区别是什么?
- 下一篇: 减脂期食谱推荐:清蒸鱼的做法是怎样的?