根号6的计算方法
作者:佚名 来源:未知 时间:2024-11-06
在数学的世界里,求解根号下的数值是一个既基础又充满奥秘的过程。当我们被问及“根号6等于多少怎么算”时,这不仅仅是一个简单的计算问题,它更是一次深入数学原理、近似计算、历史发展和实际应用等多维度的探索之旅。
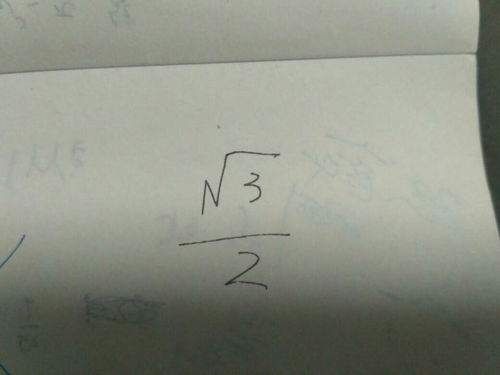
数学原理的剖析
首先,从数学原理的角度来看,根号(或称平方根)是一个数学符号,用来表示一个数的平方根。对于非负实数a,其平方根表示为√a,它满足(√a)² = a。因此,当我们要求解根号6时,我们实际上在寻找一个数,这个数的平方等于6。
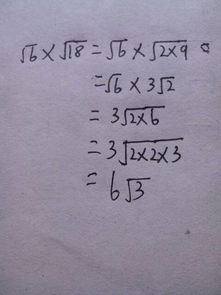
在数学上,对于不能完全开方的数(如6),我们通常无法得到一个精确的有限小数或分数答案。根号6就是这样的一个数,它的小数形式是一个无限不循环小数,即无理数。尽管我们无法直接写出一个精确的有限形式,但我们可以利用其他数学工具或方法来逼近这个值。
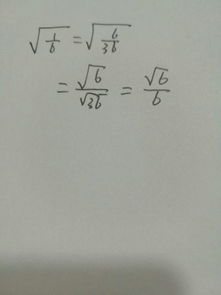
近似计算的技巧
在实际应用中,由于无理数的无限不循环特性,我们往往需要使用近似值。计算根号6的近似值有多种方法,以下列举几种常用的技巧:
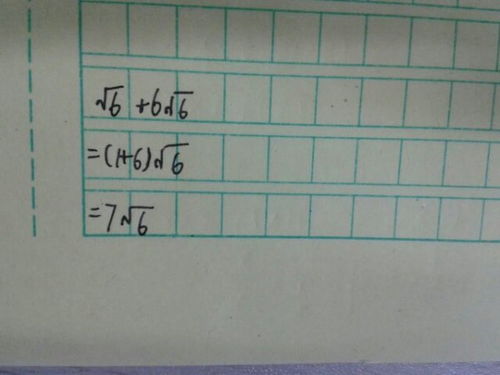
1. 使用计算器:现代计算器能够快速准确地给出根号6的近似值。这是最直接且最常用的方法,特别是在需要高精度结果时。
2. 手动开方:对于没有计算器的情况,我们可以尝试手动开方。这通常涉及到一个迭代过程,比如牛顿迭代法。虽然这种方法计算起来相对复杂,但它能让我们更好地理解平方根的性质和求解过程。
3. 连续分数逼近:连续分数是另一种逼近无理数的方法。对于根号6,我们可以找到一系列的分数,这些分数会逐渐逼近其真实值。这种方法在数学理论上有重要意义,但在实际应用中可能不如计算器直接。
4. 泰勒级数展开:对于具有解析表达式的函数,我们可以使用泰勒级数来逼近其值。根号函数也可以这样处理,通过选择合适的展开点和项数,我们可以得到一个足够精确的近似值。
历史发展的脉络
根号的概念和求解方法并不是一蹴而就的,它们经历了漫长的发展过程。早在古代,人们就开始使用各种方法来求解平方根。
古埃及和巴比伦:在这些古老文明中,人们已经掌握了求解简单平方根的方法,这些方法通常基于几何图形的构造和测量。
古希腊:毕达哥拉斯学派在研究直角三角形时,发现了无理数的存在,这标志着对数学本质理解的重大突破。根号作为表示无理数的一种方式,也随之得到了更深入的研究。
阿拉伯数学:在阿拉伯世界,数学家们进一步发展了代数和几何方法,这些方法在求解平方根和其他数学问题中发挥了重要作用。
文艺复兴时期:随着印刷术的发明和传播,数学知识得到了更广泛的传播和发展。欧洲数学家们开始系统地研究根号和其他数学符号的使用,推动了数学符号体系的完善。
现代数学:在现代数学中,根号已经成为数学分析、代数几何等多个领域不可或缺的工具。随着计算机和数值计算方法的出现,求解根号等数学问题的效率和精度都得到了极大的提升。
实际应用的广泛性
根号不仅在数学理论中占据重要地位,还在实际生活中有着广泛的应用。以下是一些具体的例子:
1. 工程学:在结构工程中,根号经常用于计算应力和应变等物理量。这些计算对于确保结构的安全性和稳定性至关重要。
2. 物理学:在物理学中,根号经常出现在能量、动量、速度等物理量的计算中。这些物理量的精确计算对于理解物理现象和解决实际问题具有重要意义。
3. 经济学和金融学:在金融领域,根号经常用于计算投资回报率的波动率和风险。这些计算有助于投资者做出明智的投资决策。
4. 计算机科学:在计算机科学中,根号在算法设计、数据分析和图像处理等领域有着广泛的应用。例如,在图像处理中,根号可以用于计算像素之间的距离和相似度等。
5. 日常生活:在日常生活中,根号也经常出现。比如,在购物时计算折扣后的价格,或者在烹饪时计算食材的比例等。虽然这些应用可能不如专业领域那么复杂,但它们同样体现了根号在日常生活中的实用性。
总结与展望
综上所述,“根号6等于多少怎么算”这个问题不仅是一个简单的数学计算问题,它还涉及到了数学原理、近似计算、历史发展和实际应用等多个方面。通过深入研究这个问题,我们可以更好地理解数学的本质和魅力,同时也能够发现数学在现实生活中的广泛应用和价值。
随着科学技术的不断发展,我们相信未来会有更多更高效的方法来求解根号等数学问题。同时,我们也期待数学能够继续为人类社会的发展和进步贡献更多的智慧和力量。在这个充满挑战和机遇的时代里,让我们携手共进,共同探索数学的奥秘和无限可能。
- 上一篇: 微信一键群发给所有好友的技巧
- 下一篇: 【图解攻略】新手必看!轻松学会新紫砂壶的完美开壶法






























