扇形的面积公式有哪三个

在数学领域，扇形面积的计算是一个基础而重要的知识点。对于许多学生来说，掌握扇形的面积公式是理解和应用几何知识的重要一环。扇形面积公式不仅在数学课堂上频繁出现，还在许多实际问题中发挥着关键作用。那么，扇形的面积公式究竟是哪三个呢？接下来，我们将详细探讨这个问题。

首先，我们要明确扇形的定义。扇形是指圆的一部分，其由两条半径和圆上的一段弧围成。扇形的面积大小取决于其圆心角的大小、半径的长度以及整个圆的面积。在计算扇形面积时，我们通常会用到以下三个主要公式：

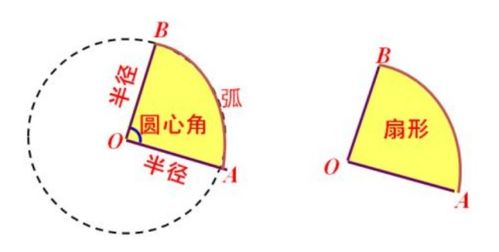
第一个公式是基于圆心角的扇形面积公式。这个公式表明，扇形的面积等于圆心角占整个圆的比例乘以圆的面积。具体地说，如果圆心角为θ（单位为弧度），半径为r，那么扇形的面积S可以表示为：S = (θ/2π) × πr²。这里，π是圆周率，r²是半径的平方。由于πr²表示整个圆的面积，因此θ/2π就是圆心角占整个圆的比例。这个公式简洁明了，适用于已知圆心角和半径时计算扇形面积的情况。

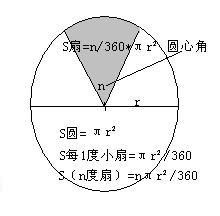
第二个公式是基于圆心角度数的扇形面积公式。在实际问题中，圆心角有时以度数表示。为了方便计算，我们可以将圆心角度数转换为弧度，然后应用第一个公式。但为了方便记忆和应用，我们也可以直接使用基于圆心角度数的扇形面积公式。具体地说，如果圆心角度数为n°，半径为r，那么扇形的面积S可以表示为：S = (n/360) × πr²。这里，360°表示一个完整的圆的角度，因此n/360就是圆心角度数占整个圆的比例。这个公式在处理以度数表示的圆心角时非常方便。

第三个公式是基于弧长的扇形面积公式。在某些情况下，我们可能已知扇形的弧长而不是圆心角。这时，我们可以使用基于弧长的扇形面积公式来计算。具体地说，如果弧长为l，半径为r，那么扇形的面积S可以表示为：S = (1/2) × l × r。这个公式的推导基于圆的性质：弧长等于圆心角对应的弧段在半径方向上的投影长度与半径的乘积。由于扇形可以看作是由弧长和两条半径围成的三角形（在极限情况下），因此其面积可以近似地看作是这个三角形的面积的一半（当弧长很短时），而在一般情况下，则通过积分等方法可以推导出上述公式。这个公式在处理已知弧长和半径时计算扇形面积的情况时非常实用。

在掌握了这三个扇形面积公式后，我们可以将它们应用到各种实际问题中。例如，在计算扇形窗户的面积时，我们可以根据窗户的弧长和半径使用基于弧长的扇形面积公式；在计算扇形蛋糕的面积时，我们可以根据蛋糕的圆心角度数和半径使用基于圆心角度数的扇形面积公式；在计算扇形花坛的面积时，我们可以根据花坛的圆心角和半径使用基于圆心角的扇形面积公式。

此外，扇形面积公式的应用还不仅仅局限于几何领域。在物理学、工程学、经济学等其他学科中，扇形面积公式也有着广泛的应用。例如，在物理学中，扇形面积公式可以用于计算电磁场中的磁通量；在工程学中，扇形面积公式可以用于计算机械零件的强度；在经济学中，扇形面积公式可以用于分析市场份额等。

需要注意的是，在使用扇形面积公式时，我们需要确保已知条件足够且准确。如果已知条件不足或存在误差，那么计算出的扇形面积也会受到影响。因此，在实际应用中，我们需要仔细审查已知条件，并选择合适的公式进行计算。

此外，扇形面积公式的推导和理解也是非常重要的。通过理解公式的推导过程，我们可以更深入地理解扇形面积的本质和计算方法。同时，这也有助于我们更好地掌握和应用其他相关的几何知识和公式。

综上所述，扇形的面积公式主要有三个：基于圆心角的扇形面积公式、基于圆心角度数的扇形面积公式和基于弧长的扇形面积公式。这三个公式在几何领域和其他学科中都有着广泛的应用。通过掌握和理解这些公式，我们可以更好地解决各种实际问题，并拓展我们的知识和视野。因此，我们应该重视扇形面积公式的学习和应用，不断提高我们的数学素养和综合能力。