如何求解三元一次方程组？

在数学的广阔领域中，解方程组是一项基础而重要的技能。尤其是三元一次方程组，它在解决实际问题的过程中发挥着关键作用。所谓三元一次方程组，是指包含三个未知数（通常记为x，y，z）和由这三个未知数构成的三个一次方程的方程组。解这类方程组不仅需要掌握基本的数学运算技巧，还需要灵活运用各种方法策略。下面，我们将从理解方程组的基本概念、选择解题方法、实际操作步骤以及解决复杂问题的策略四个维度，来探讨如何解三元一次方程组。

一、理解三元一次方程组的基本概念

三元一次方程组由三个一次方程组成，每个方程都包含三个未知数x，y，z。例如，一个简单的三元一次方程组可能如下所示：

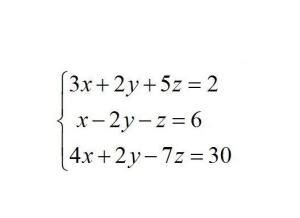
1. 2x + 3y - z = 8

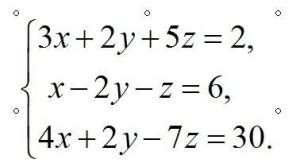
2. 4x - y + 2z = -2

3. -3x + 2y + z = 5

方程组中的每个方程代表一个平面在三维空间中的位置。解三元一次方程组的过程，就是找到同时满足这三个方程的点（即x，y，z的值），即三个平面的交点。如果方程组有唯一解，那么这三个平面会相交于一个唯一的点；如果无解，则三个平面无交点；如果方程组有无穷多解，则三个平面重合或交于一条直线。

二、选择解题方法

解三元一次方程组有多种方法，常见的有代入法、消元法和矩阵法。选择合适的方法取决于方程组的特性和个人偏好。

代入法

代入法适用于其中一个方程已经解出一个未知数的形式。例如，在上面的方程组中，如果第三个方程已经解出z为：

z = 3x - 2y + 5

就可以将这个表达式代入第一和第二个方程中，从而将三元一次方程组转化为二元一次方程组，再逐步求解。

消元法

消元法是最常用的方法之一，它通过对方程组中的方程进行加减运算，消去一个或多个未知数，从而简化方程组。例如，可以将第一个方程乘以2后与第二个方程相加，以消去z：

(2x + 3y - z) * 2 + (4x - y + 2z) = 8 * 2 - 2

简化后得到新的二元一次方程，重复此过程直到只剩下一个方程，从而解出一个未知数的值，再代入原方程组求解其他未知数。

矩阵法

矩阵法适用于处理较大规模或更复杂的方程组。它利用线性代数的知识，将方程组写成矩阵形式，通过求解矩阵的逆或行列式来找到解。矩阵法在处理多个未知数时特别有效，但要求解者具备较高的数学素养。

三、实际操作步骤

以消元法为例，具体步骤如下：

1. 观察方程组：首先观察方程组，确定哪个未知数最容易通过加减运算消去。

2. 选择方程进行运算：选择两个方程，通过乘法或除法使其中一个未知数的系数相等或互为相反数，然后相加或相减消去该未知数。

3. 重复消元：继续用剩下的方程重复上述步骤，直到只剩下一个方程和一个未知数。

4. 求解单个方程：解出剩下的方程，得到一个未知数的值。

5. 回代求解：将求得的未知数值代入原方程组，求解其他未知数。

6. 验证解：将求得的所有未知数值代入原方程组，验证它们是否满足所有方程。

四、解决复杂问题的策略

面对更复杂的三元一次方程组，可能需要结合多种方法，或采用更高级的数学工具。以下是一些解决复杂问题的策略：

1. 灵活选择方法：不要拘泥于一种方法，根据方程组的特性灵活选择代入法、消元法或矩阵法。

2. 利用软件工具：对于特别复杂或难以手动解决的方程组，可以利用数学软件（如MATLAB、Wolfram Alpha）进行求解。

3. 分解问题：将复杂问题分解为更小的、更易于管理的部分。例如，可以将三元一次方程组看作由多个二元一次方程组组成，逐步求解。

4. 检查方程组的一致性：在求解前，检查方程组是否一致（即是否有解）。如果方程组中的方程相互矛盾，则无解。

5. 培养直觉和耐心：解决复杂问题往往需要一定的直觉和耐心。通过大量练习，培养对方程组结构的敏感性和解决问题的耐心。

总之，解三元一次方程组是一个既考验基础知识又考验解题技巧的过程。通过理解基本概念、选择合适的解题方法、遵循实际操作步骤以及掌握解决复杂问题的策略，我们可以有效地解决各种类型的三元一次方程组。无论是解决日常生活中的实际问题，还是在科学研究领域进行更深入的分析，掌握这一技能都将为我们提供强大的数学支持。