正负数与分数的基本概念是什么？

在数学的世界里，数字被细致地分类，以便我们能够更精确地描述数量、大小、关系等概念。今天，我们就来深入探讨几个基础但至关重要的数字类型：正整数、负整数、正分数以及负分数。理解这些概念，将帮助我们更好地掌握数学的基石，为更复杂的数学探索打下坚实基础。

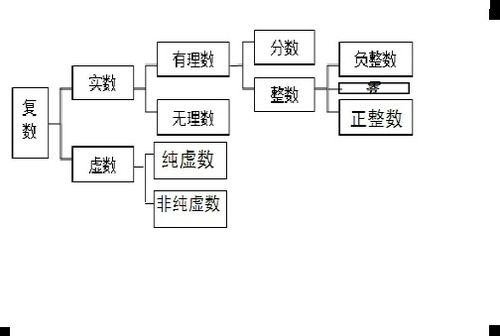
首先，我们从正整数开始。正整数，简而言之，就是大于0的整数。它们是我们在日常生活中最常使用的数字之一，用于计数、测量长度、重量、时间等。例如，1、2、3、4……都是正整数。正整数代表了一种“增多”或“增加”的概念，它们构成了一个无限的递增序列，每一个数字都比前一个数字大1。在数学运算中，正整数可以自由地进行加、减、乘、除（除数不为0）等运算，遵循着数学的基本规则。

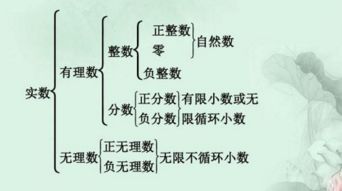
接下来，我们转向负整数的世界。负整数，顾名思义，就是小于0的整数。它们在数学中代表了一种“减少”或“亏损”的概念。负整数的符号是“-”，例如，-1、-2、-3等。当我们说一个人欠了别人5元钱时，我们可以用-5来表示这个债务。负整数的引入，使得数学能够更全面地描述现实生活中的现象，包括亏损、下降、减少等。在运算中，负整数遵循着特定的规则，如负数相加结果仍为负数，正数与负数相加结果的符号取决于绝对值较大的数，负负得正等。

现在，让我们来谈谈正分数。正分数，就是分子和分母都是正整数，并且分母不为0的有理数。它们表示了整体的一部分，或者说，是某个数量的一个比例。例如，1/2、3/4、5/6等都是正分数。正分数在数学中用于描述不完整或部分的数量，如一块蛋糕被分成两半，我们吃掉了其中的一半，就可以用1/2来表示。正分数可以参与加、减、乘、除等多种运算，运算的结果可能仍然是一个分数，也可能是一个整数，这取决于具体的运算和分数的值。

与正分数相对应的是负分数。负分数，就是分子或分母（或两者）带有负号的分数。然而，为了简化表达，我们通常将负号放在整个分数的前面，如-1/2、-3/4等。负分数表示了一种“减少”或“亏损”的比例，或者说是某个数量的一个负的部分。例如，如果我们说一个人欠了别人半个蛋糕，我们就可以用-1/2来表示这个债务。负分数在数学运算中同样遵循着特定的规则，如负分数相加、相乘的结果仍然是负分数（除非其中一个分数的负号能够相互抵消），负分数与正分数相加、相乘的结果则取决于具体的运算和分数的值。

了解了正整数、负整数、正分数和负分数的基本概念后，我们来看看它们在数学和现实生活中的应用。

在数学中，这些数字类型构成了数学运算的基础。无论是简单的算术运算，还是复杂的代数、几何、微积分等数学问题，都离不开这些数字类型的参与。例如，在解决应用题时，我们可能需要用到正整数来表示人数、物品数量等；用负整数来表示亏损、下降等；用正分数来表示比例、百分比等；用负分数来表示亏损的比例、减少的百分比等。通过巧妙地运用这些数字类型，我们可以解决各种数学问题，探索数学的奥秘。

在现实生活中，这些数字类型同样无处不在。它们帮助我们更准确地描述和计算各种现象和事件。例如，在商业领域，我们可以用正整数来表示收入、利润等；用负整数来表示支出、亏损等；用正分数来表示投资回报率、增长率等；用负分数来表示亏损率、下降比例等。在金融领域，正整数和负整数分别代表了资金的流入和流出；正分数和负分数则用于描述股价的涨跌、汇率的变动等。在科学研究中，这些数字类型更是不可或缺的工具，它们帮助我们测量、计算和分析各种实验数据和现象。

此外，这些数字类型还培养了我们的逻辑思维和数学素养。通过学习如何正确地使用这些数字类型进行运算和推理，我们可以锻炼自己的思维能力，提高解决问题的效率。同时，这些数字类型也为我们提供了更加精确和严谨的表达方式，使我们能够更好地与他人交流和沟通数学问题。

总之，正整数、负整数、正分数和负分数是数学中的基础概念，它们构成了数学运算的基石，为我们解决实际问题提供了有力的工具。通过深入理解这些概念并熟练掌握它们的运算规则，我们可以更好地掌握数学的精髓，为未来的学习和生活打下坚实的基础。同时，这些数字类型也为我们提供了一种精确、严谨和高效的表达方式，使我们能够更好地理解和描述这个世界。让我们在数学的海洋中继续探索吧！