揭秘:增长率的计算方法与奥秘
作者:佚名 来源:未知 时间:2024-11-08
增长率是经济学、统计学、财务分析等多个领域中经常使用的一个重要指标,它用于衡量某一变量在一定时期内相对于其前期水平的增长情况。了解如何计算增长率对于分析经济发展、企业业绩、人口变化等多个方面都具有重要意义。本文将从增长率的基本概念出发,详细介绍几种常见的增长率计算方法,并通过实例加以说明,以期帮助读者更好地理解和应用这一工具。
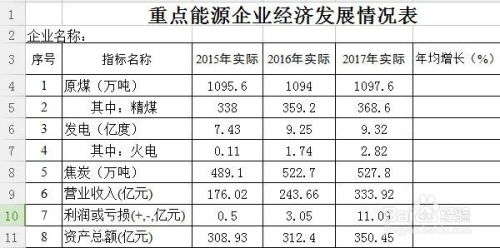
首先,我们需要明确增长率的基本概念。增长率,又称为增长比率或增长速度,是某一特定时期内的增长额与前期水平的比值,通常以百分比形式表示。增长额是指某一变量在某一时期内的绝对增加量,而前期水平则是指该变量在增长前的基准值。通过计算增长率,我们可以直观地了解某一变量在一定时期内的变化趋势和速度。
在实际应用中,增长率的计算方法因所研究对象的特性和分析目的的不同而有所差异。以下是几种常见的增长率计算方法:
一、简单增长率计算
简单增长率是最基本的增长率计算方法,适用于比较两个相邻时期的数据。其计算公式为:增长率=(本期数值-前期数值)/前期数值×100%。例如,某企业去年销售额为100万元,今年销售额为120万元,那么该企业的销售增长率为(120-100)/100×100%=20%。
二、年均增长率计算
年均增长率用于衡量某一变量在多个连续时期内的平均增长情况。其计算公式为:年均增长率=[(末期数值/初期数值)^(1/n)-1]×100%,其中n为时期数。例如,某企业连续五年的销售额分别为100万元、110万元、121万元、133.1万元和146.41万元,那么该企业的年均增长率为[(146.41/100)^(1/5)-1]×100%≈9%。
三、复合增长率计算
复合增长率是另一种常用的增长率计算方法,它考虑了多个时期内的连续增长情况。其计算公式为:复合增长率=[(末期数值/初期数值)^(1/年数)-1],其中年数是指计算复合增长率所涵盖的时期数(以年为单位)。需要注意的是,复合增长率在计算过程中使用了连乘和开方运算,因此也被称为几何平均增长率。例如,某股票在连续三年内的价格分别为10元、12元和15元,那么该股票的复合增长率为[(15/10)^(1/3)-1]≈14.47%。
四、环比增长率计算
环比增长率用于衡量某一变量在相邻两个时期内的增长情况。其计算公式为:环比增长率=(本期数值-上期数值)/上期数值×100%。与简单增长率相比,环比增长率更注重分析变量的短期波动情况。例如,某商品在上月的销售量为1000件,本月销售量为1200件,那么该商品的环比增长率为(1200-1000)/1000×100%=20%。
五、同比增长率计算
同比增长率用于衡量某一变量在某一时期与上一年相同时期内的增长情况。其计算公式为:同比增长率=(本期数值-同期数值)/同期数值×100%。同比增长率有助于消除季节性因素对数据分析的影响,因此常被用于经济数据的分析中。例如,某地区今年一季度GDP为1000亿元,去年同期GDP为900亿元,那么该地区的同比增长率为(1000-900)/900×100%≈11.11%。
在了解了增长率的计算方法后,我们还需要注意以下几点以确保计算的准确性和有效性:
1. 数据的选择与处理:在计算增长率时,应确保所使用数据的准确性和可比性。对于异常值或缺失值,应进行合理处理或剔除。
2. 基期的选择:基期是计算增长率的起点,选择合适的基期对于准确反映变量的增长情况至关重要。一般来说,基期应选择具有代表性的时期。
3. 增长率的解释与应用:增长率只是一个相对指标,它反映了变量的增长速度而非绝对水平。因此,在解释和应用增长率时,应结合变量的绝对水平和变化趋势进行综合分析。
4. 增长率的局限性:增长率虽然是一个有用的分析工具,但它也具有局限性。例如,增长率无法反映变量的内部结构变化;对于周期性波动较大的变量,增长率可能会产生误导性信息。因此,在使用增长率时,应充分考虑其适用范围和局限性。
通过以上介绍,我们可以发现增长率是一个广泛应用于多个领域的分析工具。它不仅可以用于衡量经济发展、企业业绩等方面的增长情况,还可以用于预测未来趋势、制定发展策略等。因此,掌握增长率的计算方法并正确应用它对于提高我们的数据分析能力和决策水平具有重要意义。
总之,增长率是一个简单而有效的分析工具,它可以帮助我们更好地了解变量的增长情况和变化趋势。在计算增长率时,我们应选择合适的计算方法并注意数据的准确性和可比性;在解释和应用增长率时,我们应结合变量的绝对水平和变化趋势进行综合分析;同时,我们还应
- 上一篇: 如何登录山东省教育云服务平台
- 下一篇: 留学海外需满足哪些条件?













































