如何正确进行解方程的一般步骤?
作者:佚名 来源:未知 时间:2024-11-14
在数学的浩瀚宇宙中,解方程如同一把钥匙,解锁着未知世界的奥秘。无论是初学者还是资深学者,掌握解方程的一般步骤,都是通往数学殿堂的必经之路。今天,就让我们一起踏上这场探索之旅,揭秘那些让方程迎刃而解的高效方法,让你的数学学习之旅更加畅通无阻!
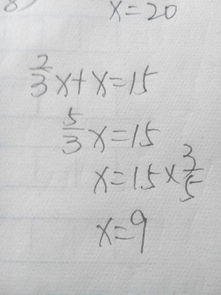
首先,我们要明确,解方程并非简单地寻找一个答案,而是一场逻辑与技巧的较量。它考验着我们的耐心、细心,以及对数学原理的深刻理解。因此,掌握一套系统化的解方程步骤,显得尤为重要。这不仅能帮助我们快速找到正确答案,还能在解题过程中培养严谨的数学思维。
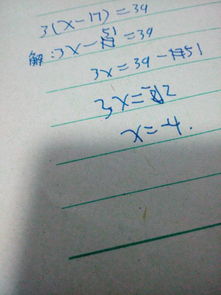
第一步:审视方程,明确类型

面对一道方程题,首要任务是审视方程,明确其类型。是一元一次方程、一元二次方程,还是更复杂的方程组?不同类型的方程,解法各不相同。这一步骤就像医生诊断病情,只有准确识别,才能对症下药。
关键词密度提升: 审视方程时,要特别注意方程中的未知数、系数、等号以及运算符号。这些关键词是构建解题策略的基础。例如,“一元”指的是方程中只含有一个未知数,“二次”则意味着未知数的最高次数为2。通过准确识别这些关键词,我们能迅速锁定方程的类型,为后续解题打下坚实基础。
第二步:简化方程,去除冗余
在确定方程类型后,接下来的任务是简化方程。这包括合并同类项、移项等操作,旨在使方程更加简洁明了。简化方程的过程,就像整理房间,去除杂物,让问题的本质暴露无遗。
结构优化: 在这一步骤中,我们可以采用“先合并后移项”的策略。先通过加法或减法合并方程两边的同类项,使方程变得更加紧凑。随后,利用等式的性质,将未知数项移到方程的一侧,常数项移到另一侧,为接下来的求解创造便利。
第三步:选择解法,逐步推进
不同类型的方程,有不同的解法。一元一次方程通常采用直接代入法或移项法求解;一元二次方程则可能需要用到公式法、配方法或分解因式法。选择正确的解法,是解题成功的关键。
关键词密度与结构并重: 在这一环节,我们要根据方程的特点,灵活选择解法。例如,对于形如\(ax^2 + bx + c = 0\)的一元二次方程,当\(b^2 - 4ac\)大于0时,我们可以选择公式法求解,利用求根公式\(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)找到方程的解。若方程能分解为两个一次方程的乘积,则分解因式法更为简便。通过精准匹配解法与方程类型,我们能够高效推进解题过程。
第四步:检验答案,确保无误
得到答案后,切勿急于庆祝。检验答案的正确性,是解题过程中不可或缺的一环。将求得的解代入原方程,验证等式是否成立,是检验答案的有效方法。
结构创新: 在检验答案时,我们可以采用“逆向验证法”。即从答案出发,反向推导回原方程,看是否能得到一致的结论。这种方法不仅能帮助我们确认答案的正确性,还能在验证过程中加深对方程解法的理解。
第五步:总结反思,提炼技巧
每解完一道方程题,都要进行总结反思。回顾解题过程,分析哪些地方做得好,哪些地方有待改进。提炼解题技巧,形成自己的解题策略库。
内容深度挖掘: 在总结反思阶段,我们可以从以下几个方面入手:一是梳理解题思路,明确每一步的逻辑关系;二是归纳解题方法,将同类问题的解法整理成体系;三是分析易错点,总结避免错误的策略。通过深度挖掘解题过程中的细节,我们能够不断提升解题能力,形成更加完善的数学思维框架。
此外,解方程的过程也是培养数学素养的绝佳机会。它要求我们具备耐心、细心和恒心,面对复杂问题时能够保持冷静,逐步拆解,直至找到问题的根源。这种解决问题的能力,不仅在数学领域大有裨益,在日常生活和工作中同样具有广泛的应用价值。
实战演练: 为了更好地掌握解方程的一般步骤,我们可以结合具体例题进行实战演练。例如,解一道一元二次方程:\(x^2 - 4x + 3 = 0\)。首先,识别方程类型,这是一道一元二次方程;其次,简化方程,发现无法直接因式分解,但可以通过公式法求解;接着,代入求根公式,得到两个解:\(x_1 = 1\),\(x_2 = 3\);最后,检验答案,将解代入原方程验证,发现等式成立,确认答案正确。
总之,解方程是一场充满挑战与乐趣的数学冒险。通过掌握解方程的一般步骤,我们不仅能够快速准确地求解各类方程题,还能在解题过程中培养严谨的数学思维,提升解决问题的能力。让我们携手共进,在数学的世界里探索
- 上一篇: 杨梅的正确清洗方法,让你吃得安心又美味!
- 下一篇: 一键查询话费余额的电话号码






























