三角函数正弦如何转换为余弦公式是什么?
作者:佚名 来源:未知 时间:2024-11-13
三角函数是数学中的一个重要分支,广泛应用于物理、工程、计算机科学等领域。其中,正弦函数和余弦函数是最为基础和重要的两种三角函数。在实际应用中,我们经常需要在正弦和余弦之间进行转换,这就涉及到一些特定的公式和技巧。本文将详细介绍三角函数正弦和余弦的转换公式,并探讨它们的应用和推导过程。
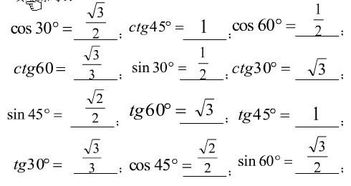
首先,我们需要了解正弦函数和余弦函数的定义。正弦函数sin(x)定义为对边与斜边之比,在直角三角形中,sin(x) = 对边/斜边。而余弦函数cos(x)则定义为邻边与斜边之比,即cos(x) = 邻边/斜边。这里的x是锐角或与锐角对应的弧度值。
转换公式的基础
正弦和余弦之间的转换公式主要基于以下几个基础关系:
1. 平方和公式:这是最基本的关系之一,对于任意角度x,都有sin²(x) + cos²(x) = 1。这个公式可以看作是正弦和余弦函数在几何上的直观表现,它揭示了正弦和余弦值之间的互补关系。
2. 诱导公式:三角函数在不同的象限具有不同的符号和大小关系。利用诱导公式,我们可以将任意角度的三角函数值转化为锐角范围内的三角函数值。例如,对于第二象限的角度,sin(π - x) = sin(x),cos(π - x) = -cos(x)。这些公式在解决复杂问题时非常有用。
3. 互余角公式:在直角三角形中,如果两个角是互余的(即它们的和为90度),那么它们的正弦和余弦值有特定的关系。具体来说,对于互余角x和y(x + y = 90°),有sin(x) = cos(y)和cos(x) = sin(y)。这个公式揭示了正弦和余弦函数在互余角上的对称性。
具体转换公式
基于上述基础关系,我们可以推导出一些具体的正弦和余弦转换公式:
1. 正弦转余弦公式:
如果我们已知sin(x)的值,想要找到cos(x)的值,可以直接使用平方和公式:cos(x) = ±√(1 - sin²(x))。这里的正负号取决于x所在的象限。
另一种方法是利用互余角公式。如果x是锐角,那么cos(x) = sin(90° - x)。
2. 余弦转正弦公式:
类似地,如果已知cos(x)的值,我们可以使用平方和公式找到sin(x)的值:sin(x) = ±√(1 - cos²(x))。同样,正负号取决于x所在的象限。
或者利用互余角公式:sin(x) = cos(90° - x)。
3. 利用诱导公式进行转换:
诱导公式可以帮助我们将任意角度的三角函数值转化为已知角度的三角函数值。例如,对于第二象限的角度x,我们可以利用sin(π - x) = sin(x)和cos(π - x) = -cos(x)进行转换。
对于其他象限的角度,也可以利用类似的诱导公式进行转换。
推导过程与示例
为了更好地理解这些公式,我们可以通过具体的例子来推导它们:
1. 平方和公式的推导:
考虑一个直角三角形,设其锐角为x,对边为a,邻边为b,斜边为c。根据勾股定理,我们有a² + b² = c²。
将正弦和余弦的定义代入上式,得到sin²(x) + cos²(x) = (a/c)² + (b/c)² = (a² + b²)/c² = c²/c² = 1。
2. 互余角公式的推导:
考虑两个互余的锐角x和y,它们构成一个直角三角形。在这个三角形中,x的对边是y的邻边,x的邻边是y的对边。
因此,我们有sin(x) = a/c = b/c的邻边 = cos(y),以及cos(x) = b/c = a/c的对边 = sin(y)。
3. 示例计算:
假设已知sin(30°) = 1/2,我们需要找到cos(30°)的值。
使用平方和公式:cos(30°) = ±√(1 - sin²(30°)) = ±√(1 - (1/2)²) = ±√(3/4) = ±√3/
- 上一篇: 密胺材料解析:用作餐具是否安全无毒?
- 下一篇: 鸿是江边鸟,下一句是什么揭秘






























