如何高效使用median函数及其实际案例解析
作者:佚名 来源:未知 时间:2024-11-10
median函数使用方法及实例
在数据分析与处理中,median(中位数)是一个非常重要的统计量。与均值(mean)相比,中位数对于偏斜分布的数据更具鲁棒性,能够更好地反映数据的中心趋势。本文将详细介绍median函数的使用方法,并通过实例展示其在不同场景下的应用。
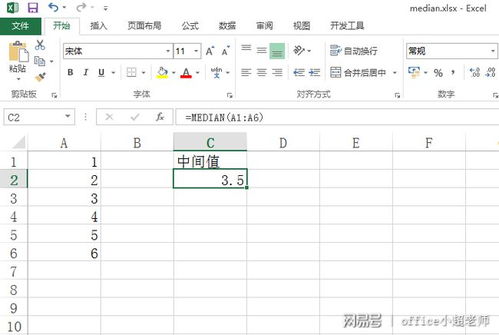
一、median函数的基本概念
中位数是指将一个数据集中的数值按照大小顺序排列后,位于中间位置的数值。如果数据集的个数是奇数,则中位数就是中间那个数;如果数据集的个数是偶数,则中位数是中间两个数的平均值。中位数的优点在于,它对极端值(即数据集中的最大值或最小值)不敏感,因此适用于处理具有偏斜分布的数据集。
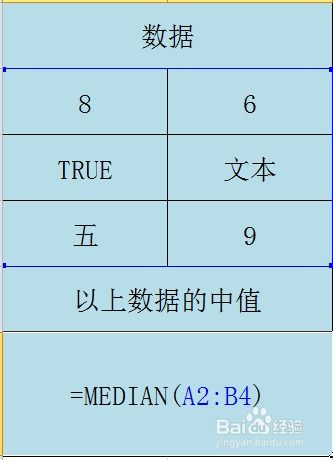
二、median函数在不同软件中的使用方法
1. Excel中的MEDIAN函数
Excel中的MEDIAN函数用于计算一组数据的中位数。
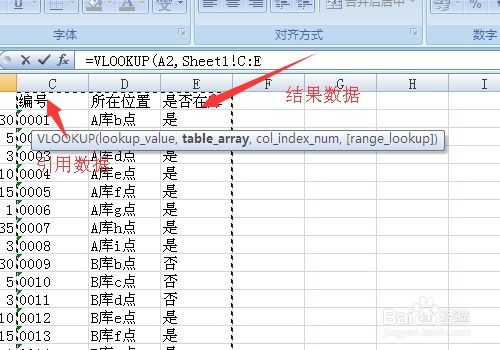
语法:`MEDIAN(number1, [number2], ...)`
参数:`number1, number2, ...` 为需要计算中位数的1到255个数值。
示例:
假设在Excel中有以下一组数据:A1=5,A2=3,A3=8,A4=1,A5=7。
在B1单元格中输入公式:`=MEDIAN(A1:A5)`,按下回车键后,B1单元格将显示5,这就是这组数据的中位数。
2. Python中的median函数
在Python中,可以通过NumPy库来计算中位数。NumPy是一个强大的科学计算库,提供了大量的数学函数和操作。
安装NumPy:如果还没有安装NumPy,可以使用pip命令进行安装:`pip install numpy`
导入NumPy库:`import numpy as np`
使用np.median函数:`np.median(a, axis=None, out=None, overwrite_input=False, keepdims=)`
参数说明:
`a`:输入数组。
`axis`:沿指定轴计算中位数。如果为None,则计算整个数组的中位数。
`out`:可选参数,用于存放结果的数组。
`overwrite_input`:如果为True,则允许在计算过程中修改输入数组。
`keepdims`:如果为True,则保持输出数组的维度与输入数组相同。
示例:
```python
import numpy as np
创建一个一维数组
data = np.array([5, 3, 8, 1, 7])
计算中位数
median_value = np.median(data)
print("中位数是:", median_value)
```
输出结果将是:
```
中位数是: 5.0
```
3. R语言中的median函数
R语言是一种用于统计计算和图形的编程语言和软件环境。在R中,可以直接使用median函数来计算中位数。
语法:`median(x, na.rm = FALSE)`
参数:
`x`:数值向量或数组。
`na.rm`:如果为TRUE,则忽略NA值。
示例:
```R
创建一个数值向量
data <- c(5, 3, 8, 1, 7)
计算中位数
median_value <- median(data)
print(paste("中位数是:", median_value))
```
输出结果将是:
```
[1] "中位数是: 5"
```
三、median函数的应用实例
实例1:分析考试成绩
假设有一组学生的考试成绩,我们需要计算这组成绩的中位数来评估学生的平均表现。
Excel实现:
在Excel中,将数据输入到一列中,然后使用MEDIAN函数计算中位数。
Python实现:
```python
import numpy as np
输入考试成绩
scores = np.array([85, 78, 92, 66, 88, 79, 94, 80, 77, 69])
计算中位数
median_score = np.median(scores)
print("考试成绩的中位数是:", median_score)
```
输出结果将是:
```
考试成绩的中位数是: 80.5
```
实例2:处理偏斜分布数据
在处理某些具有偏斜分布的数据时,中位数比均值更能反映数据的真实情况。例如,分析一个公司的收入数据时,如果数据中存在极端高收入值,则使用中位数更能代表大多数
- 上一篇: 揭秘:虚荣心究竟是什么?
- 下一篇: 同城急送,轻松叫跑腿!






























