乘法的基本概念及其重要性解析
作者:佚名 来源:未知 时间:2024-11-11
乘法的概念和意义
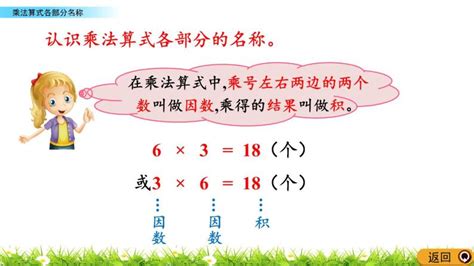
在数学的广阔天地里,乘法作为四则运算之一,扮演着举足轻重的角色。它不仅仅是数字之间的简单相乘,更蕴含着深刻的数学思想和广泛的应用价值。本文旨在深入探讨乘法的概念和意义,帮助读者更好地理解这一基础而重要的数学概念。
一、乘法的概念
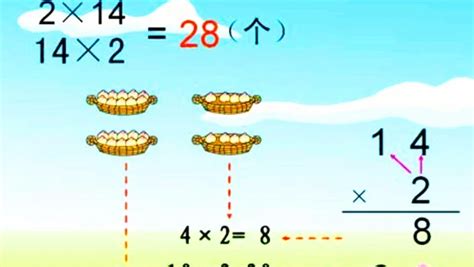
乘法,顾名思义,是一种通过重复加法来实现数值增长的运算方式。简单来说,乘法就是将一个数(被乘数)重复加自己某一次数(乘数)所得到的和。例如,3乘以4,可以理解为4个3相加,即3+3+3+3=12。这种定义方式直观且易于理解,适用于初学者掌握乘法的基本概念。
然而,乘法并不仅限于这种直观的加法重复。在更抽象的数学领域中,乘法被赋予了更丰富的内涵。它可以表示集合中元素的组合方式,可以描述几何图形的变换,还可以作为线性代数、矩阵运算等高级数学工具的基础。这些高级应用虽然超出了初学者的理解范围,但却展示了乘法在数学体系中的广泛性和深刻性。
二、乘法的运算规则
乘法运算遵循一系列基本的规则,这些规则构成了乘法运算的基础框架。
1. 交换律:乘法满足交换律,即乘数与被乘数的顺序可以互换而不影响结果。例如,3乘以4等于4乘以3,即3×4=4×3。
2. 结合律:乘法还满足结合律,即多个数相乘时,改变它们的结合方式不会影响最终结果。例如,(2×3)×4等于2×(3×4),即(2×3)×4=2×(3×4)。
3. 零乘法:任何数与0相乘都等于0。这是乘法运算中的一个重要性质,它揭示了0在乘法运算中的特殊地位。
4. 单位元:任何数与1相乘都等于它本身。这里的1被称为乘法的单位元,它是乘法运算中的另一个关键元素。
5. 分配律:乘法对加法满足分配律,即一个数与两个数的和相乘,等于这个数分别与这两个数相乘后的和。例如,a×(b+c)等于a×b+a×c。分配律是乘法与加法之间的重要联系纽带,它在数学运算和问题解决中发挥着重要作用。
三、乘法的实际应用
乘法不仅在数学理论中占据重要地位,还在现实生活中有着广泛的应用。
1. 计数与测量:在日常生活中,我们经常需要用到乘法来计数或测量。例如,在购买物品时,我们需要知道单价和数量来计算总价;在计算面积或体积时,我们也需要用到乘法。这些实际应用展示了乘法在日常生活中的实用性和重要性。
2. 时间与速度:在物理学中,乘法被用来计算时间和速度之间的关系。例如,如果我们知道一个物体的速度和它移动的时间,我们就可以用乘法来找出它移动的距离。这种应用不仅限于物理学领域,还广泛存在于日常生活和工作中。
3. 比例与比例关系:乘法在描述比例和比例关系中起着关键作用。例如,在绘制地图或图表时,我们需要用乘法来确定不同元素之间的比例关系;在制定预算或计划时,我们也需要用到乘法来估算成本和资源需求。
4. 金融与投资:在金融和投资领域,乘法被用来计算利息、复利、收益率等关键指标。这些计算不仅涉及到个人的财务规划和管理,还关系到整个经济体系的稳定和发展。
5. 工程与科学计算:在工程和科学计算中,乘法被广泛应用于各种公式的推导和计算中。例如,在力学中计算力和加速度之间的关系时;在电磁学中计算电流和电压之间的关系时;在化学中计算分子量和摩尔质量时等等。这些应用展示了乘法在科学技术领域的广泛性和重要性。
四、乘法的教育意义
乘法作为数学教育中的重要内容之一,对学生的思维发展和问题解决能力有着深远的影响。
1. 培养抽象思维能力:乘法运算涉及到数字、符号和公式的组合与变换,这要求学生具备较高的抽象思维能力。通过学习乘法,学生可以逐渐掌握这种思维方式,从而更好地理解和解决数学问题。
2. 提高运算效率:相对于加法而言,乘法运算更加高效和简洁。掌握乘法运算可以帮助学生更快地解决复杂的数学问题,提高他们的计算能力和解题效率。
3. 培养逻辑推理能力:乘法运算遵循一系列严格的规则和性质,这要求学生具备较强的逻辑推理能力来理解和运用这些规则。通过学习乘法,学生可以锻炼自己的逻辑推理能力,从而更好地理解和解决数学问题以及其他领域的问题。
4. 增强数学学习兴趣:乘法运算具有丰富的实际应用背景和趣味性强的数学问题,这可以激发学生的学习兴趣和好奇心。通过学习乘法并解决相关的问题,学生可以感受到数学的魅力和乐趣,从而更加积极地投入到数学学习中去。
五、结语
综上所述,乘法作为数学中的基础运算之一,具有广泛的应用价值和深刻的教育意义。它不仅在数学理论中占据重要地位
- 上一篇: 百分数核心知识点概览
- 下一篇: 电信积分兑换指南:轻松查找兑换地点






























