轻松掌握十字相乘法,快速解题秘籍
作者:佚名 来源:未知 时间:2024-11-11
十字相乘法教程
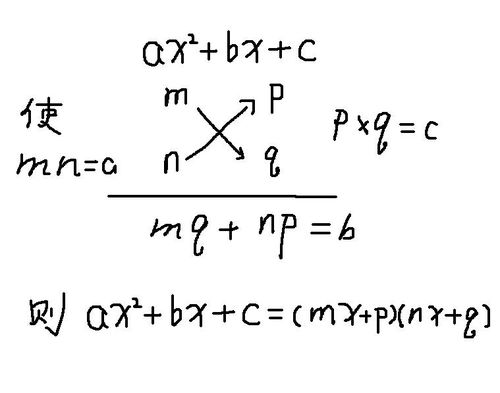
十字相乘法的方法简单来说就是:十字左边相乘等于二次项系数,右边相乘等于常数项,交叉相乘再相加等于一次项系数。十字相乘法的用处:(1)解方程;(2)因式分解;(3)解不等式。
十字相乘法是因式分解中较常用的方法,十字相乘法解式的具体方法简单明了。
十字分解法的方法简单来讲就是:十字左边相乘等于二次项系数,右边相乘等于常数项,交叉相乘再相加等于一次项系数。其实就是运用乘法公式(x+a)(x+b)=x²+(a+b)x+ab的逆运算来进行因式分解。
十字相乘法能把某些二次三项式分解因式。这种方法的关键是把二次项系数a分解成两个因数a1,a2的积,使a1b+a2c正好是一次项的系数b,那么可以直接写成结果:ax²+bx+c=(a1x+c1)(a2x+c2)。在运用这种方法分解因式时,要注意观察,尝试,并体会它实质是二项式乘法的逆过程。当首项系数不是1时,通常需要多次试验,务必注意各项系数的符号。
基本式子:x²+(p+q)x+pq=(x+p)(x+q)。
例1:把m²+4m-12分解因式。
解:本题中常数项-12可以分解为-2×6,-3×4,-4×3,-6×2,-12×1。经过尝试,发现-2×6分解后满足条件。
即m²+4m-12=(m+6)(m-2)。
例2:解方程:x²+x-6=0。
解:把常数项-6进行因式分解,得-6=(-2)×3=(-3)×2=(-6)×1=(-1)×6。尝试后可得-2×3满足条件。
因此原方程可化为(x-2)(x+3)=0。
解得:x1=2,x2=-3。
总结:
十字相乘法能把某些二次三项式ax²+bx+c(a≠0)分解因式。这种方法的关键是把二次项系数a分解成两个因数a1,a2的积a1·a2,使a1b+a2c正好是一次项的系数b,那么可以直接写成结果:ax²+bx+c=(a1x+c1)(a2x+c2)、在运用这种方法分解因式时,要注意观察,尝试,并体会它实质是二项式乘法的逆过程。当首项系数不是1时,通常需要多次试验,务必注意各项系数的符号。
十字相乘法多用于二次三项式(一元二次式)的分解因式(不一定是整数范围内)。
具体方法:
1、十字相乘法能把某些二次三项式ax²+bx+c(a≠0)分解因式。这种方法的关键是把二次项系数a分解成两个因数a1,a2的积a1·a2,使a1b+a2c正好是一次项的系数b,那么可以直接写成结果:ax²+bx+c=(a1x+c1)(a2x+c2)、在运用这种方法分解因式时,要注意观察,尝试,并体会它实质是二项式乘法的逆过程。当首项系数不是1时,通常需要多次试验,务必注意各项系数的符号。
2、具体操作过程:通过看常数项确定能分解成两个因数的积,而后根据十字相乘法:十字左边相乘等于二次项系数,右边相乘等于常数项,交叉相乘再相加等于一次项系数。
原理:
一个集合中的个体,只有2个不同的取值,部分个体取值为A,剩余部分取值为B。平均值为C。求取值为A的个体与取值为B的个体的比例。假设总量为单位1。
由:(1)平均值的公式 C=A所占的比例×A+B所占的比例×B;
(2)A所占的比例+B所占的比例=1;
得:(3)设A所占的比例为x,则B所占的比例为1-x。
代入(1)式得:C=x×A+(1-x)×B;
整理得:(4)x=(C-B)/(A-B);
十字相乘法就是使用上述原理,在多项式系数所组成的矩阵中,寻找因数的方法。
如:把x²+6x-16分解因式,十字相乘后得:
1x 8
- 上一篇: 如何求解平面的法向量
- 下一篇: 怎样有效杀死苍蝇卵?






























