探索集合的奥秘:并集、交集、全集与补集的区别详解
作者:佚名 来源:未知 时间:2024-11-12
在我们日常生活中,无论是整理书架上的书籍,还是挑选餐厅里的菜单,我们都在不自觉地运用着集合的概念。集合论,这个看似高大上的数学分支,其实与我们的生活息息相关。今天,我们就来聊聊集合论中的几个基本概念:并集、交集、全集和补集。通过一些生动的例子,帮助大家更好地理解这些概念,并区分它们之间的不同。
想象一下,你有一个书架,上面摆满了各种类型的书籍:小说、科幻、历史、传记等。这些不同类型的书籍,就像是不同的集合。现在,我们来逐一看看这些集合概念是如何应用的。
并集:合并的力量
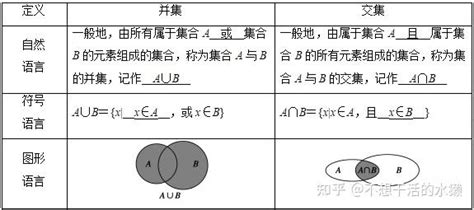
首先,我们来看看并集。并集,简单来说,就是把两个或多个集合中的所有元素合并在一起,形成一个新的集合。就像你把书架上的小说和历史书籍都拿出来,放在一起,形成一个新的书籍集合一样。
举个例子,假设有两个集合:
集合A:{苹果,香蕉,橙子}
集合B:{橙子,葡萄,西瓜}
那么,集合A和集合B的并集就是:{苹果,香蕉,橙子,葡萄,西瓜}。你看,并集就像是把所有元素都“并”到了一起,没有重复,也没有遗漏。
交集:共同的交集
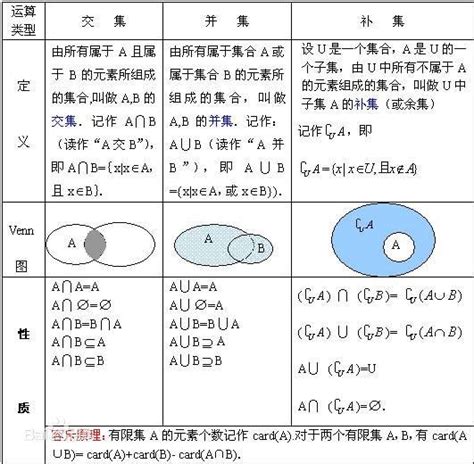
接下来,我们聊聊交集。交集,是指两个或多个集合中都有的元素组成的集合。就像你在书架上找到一本同时属于小说和历史类别的书(虽然这种情况比较少见,但假设存在),这本书就是小说集合和历史集合的交集。
回到我们之前的例子:
集合A:{苹果,香蕉,橙子}
集合B:{橙子,葡萄,西瓜}
集合A和集合B的交集就是:{橙子}。因为橙子是唯一同时出现在集合A和集合B中的元素。
交集的概念在生活中也很常见。比如,你和你的朋友可能都喜欢某些电影或音乐,这些共同喜欢的作品就是你们兴趣爱好的交集。
全集:包罗万象
全集,是一个包含所有可能元素的集合。在集合论中,全集通常被记作U(大写字母U,代表Universe,即宇宙,意味着包含一切)。就像你的书架上的所有书籍,无论是什么类型,都属于你的书籍全集。
全集的概念是相对的。比如,在谈论水果的时候,全集可能是所有种类的水果;但在谈论书籍的时候,全集就是所有类型的书籍。重要的是理解,全集是特定情境下所有可能元素的集合。
补集:缺失的部分
最后,我们来谈谈补集。补集,是指在一个全集U中,但不在某个特定集合A中的所有元素组成的集合。就像你的书架上有很多书,但如果你只关注小说类别,那么那些不是小说的书籍,就是小说集合的补集。
举个例子,假设全集U是:{苹果,香蕉,橙子,葡萄,西瓜,菠萝}
而集合A是:{苹果,香蕉,橙子}
那么,集合A在全集U中的补集就是:{葡萄,西瓜,菠萝}。这些元素都在全集U中,但不在集合A中。
补集的概念在数据分析、统计学等领域有着广泛的应用。比如,在市场调研中,了解某个产品或服务的非用户群体(即用户群体的补集),对于制定营销策略至关重要。
生活中的集合论
现在,让我们来看看这些集合概念在生活中的实际应用。
假设你正在计划一个周末的户外活动。你邀请了你的朋友小李和小张。小李喜欢徒步和钓鱼,而小张喜欢钓鱼和露营。
我们可以把“喜欢徒步”看作一个集合A,包含小李;
把“喜欢钓鱼”看作一个集合B,包含小李和小张;
把“喜欢露营”看作一个集合C,包含小张。
那么,集合A和集合B的并集,就是喜欢徒步或钓鱼的人,即小李和小张(因为小张虽然不喜欢徒步,但喜欢钓鱼,所以也在并集中);
集合B和集合C的交集,就是喜欢钓鱼和露营的人,即小张;
假设全集U是你的所有朋友(包括小李和小张,以及其他可能的朋友),那么集合B(喜欢钓鱼的人)的补集,就是不喜欢钓鱼的人,即那些不在集合B中的朋友。
通过这样的例子,我们可以看到,集合论不仅是一个抽象的数学概念,它还能帮助我们更好地理解和分析现实世界中的复杂关系。
总结
并集,是把两个或多个集合中的所有元素合并在一起,形成一个新的集合;
交集,是指两个或多个集合中都有的元素组成的集合;
全集,是一个包含所有可能元素的集合,是特定情境下所有元素的集合;
补集,是指在一个全集U中,但不在某个特定集合A中的所有元素组成的集合。
这些集合概念,就像是我们思维中的工具箱,帮助我们更好地组织和理解信息。无论是在日常生活中整理物品,还是在工作中分析数据,掌握这些概念都能让我们更加
- 上一篇: 火车票上的“杭州站”具体指哪个站点?
- 下一篇: 完美烤生蚝的详细制作步骤






























