什么是质因数？

在数学的世界里，有许多既基础又迷人的概念，它们如同构建知识大厦的砖石，为更复杂的理论提供坚实的支撑。今天，我们就来探讨这样一个概念——质因数。质因数，这个名词听起来或许有些专业，但实际上，它与我们日常生活中的许多事物息息相关，理解它，不仅能加深我们对数学的认识，还能帮助我们在解决实际问题时找到更为简洁高效的途径。

一、质数与合数的概念回顾

在正式介绍质因数之前，让我们先回顾一下两个基础概念：质数和合数。

质数，是一个大于1的自然数，它只有两个正因数：1和它本身。换句话说，质数是不能被其他自然数（除了1和它本身）整除的数。例如，2、3、5、7、11等都是质数。质数在数学中扮演着特殊而重要的角色，它们构成了数论研究的核心之一。

与质数相对应的是合数。合数是一个大于1的自然数，并且除了1和它本身外，还有其他正因数。比如，4、6、8、9等都是合数，因为除了1和它们自身外，还可以被其他数整除。

二、质因数的定义与性质

当我们理解了质数和合数后，质因数的概念就变得清晰起来。质因数，简单来说，就是一个数的因数，且这个因数本身是质数。换句话说，如果一个数A可以被另一个质数B整除，那么B就是A的一个质因数。

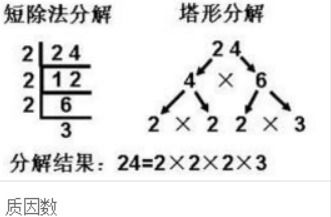
举个例子，数字12的因数有1、2、3、4、6和12。在这些因数中，只有2和3是质数。因此，2和3就是12的质因数。而4、6和12虽然不是12的唯一因数，但它们不是质数，所以不被视为质因数。

质因数具有几个重要的性质：

1. 唯一性：每个合数都可以表示为若干个质因数的乘积，并且这种表示方式是唯一的（不考虑因数的顺序）。这就是著名的质因数分解定理，它是数论中的一个基本定理。例如，数字30可以分解为2×3×5，这三个质因数相乘得到30，且这种分解方式是唯一的。

2. 最小性：对于任何大于1的正整数n，它的最小质因数一定不大于√n（n的平方根）。这个性质在寻找一个数的质因数时非常有用，因为它可以帮助我们缩小搜索范围。

3. 乘积性：如果两个数a和b的质因数分别是p1, p2, ..., pk和q1, q2, ..., qm，那么a×b的质因数就是p1, p2, ..., pk, q1, q2, ..., qm（去除重复的）。这个性质说明了质因数在乘法运算中的传递性。

三、质因数分解的方法与应用

质因数分解，即将一个合数表示为若干个质因数的乘积的过程，是数学中的一个重要技能。它不仅有助于我们深入理解数的结构，还在实际生活中有着广泛的应用。

分解方法

1. 试除法：从最小的质数2开始，依次用每个质数去除待分解的数，如果能整除，则记录下这个质数，并用商继续尝试分解，直到商为质数为止。这种方法虽然直观，但对于较大的数来说，效率较低。

2. 筛选法：对于一系列数，通过预先筛选出其中的质数，然后在分解时只考虑这些质数。这种方法在处理大量数时更为高效。

3. pollard's rho算法：一种适用于大数的质因数分解算法，它通过构造一个伪随机数序列来寻找非平凡因子。虽然理解起来较为复杂，但在计算机科学和密码学中有着重要应用。

应用领域

1. 密码学：许多加密算法，如RSA加密算法，都依赖于质因数分解的困难性来保障数据的安全性。如果质因数分解变得容易，这些加密算法的安全性将受到严重威胁。

2. 计算机科学：在编程中，质因数分解常用于优化算法，比如判断一个数是否为质数、计算两个数的最大公约数（GCD）等。此外，在图论、组合数学等领域也有广泛应用。

3. 物理学：在量子力学和统计力学中，质因数分解有助于理解某些物理现象的规律，如粒子的能级分布等。

4. 经济学：在经济学和金融学中，质因数分解可以用于分析经济增长的源泉、评估投资项目的风险等。

四、质因数与日常生活的联系

质因数不仅仅停留在数学课本上，它与我们的日常生活也紧密相连。比如，当我们需要将一块蛋糕均匀地分给一定数量的朋友时，了解蛋糕的总块数和朋友的数量之间的质因数关系，可以帮助我们更高效地切割和分配蛋糕。

再比如，在设计密码时，利用质因数分解的困难性，我们可以创建出更加安全的密码系统